Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 7

Тогда уравнение (3.26) можно привести к следующему безразмерному виду:

t = ræ²у²,      = t /t_ст = æ²h²(dj /dh)² ,          (3.29)

или с учетом того, что t » t_ст,

hæ = 1;                                          (3.30)

dj = (1/æ)dh/h; 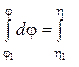  (1/æ)dh/h ,                       (3.31)

где индексом «l» обозначены величины, относящиеся к границе ламинарного подслоя при у = у₁; h = h₁; j = j₁. При этом на внешней границе подслоя в соответствии с (3.25) j₁ = h₁. Тогда уравнение (3.31) можно переписать в виде

j = (1/æ)1n h + C,                                 (3.32)

где С = h₁ – (1/æ)ln h₁.

Это и есть универсальный логарифмический профиль скорости в турбулентном пограничном слое (рис. 3.11).

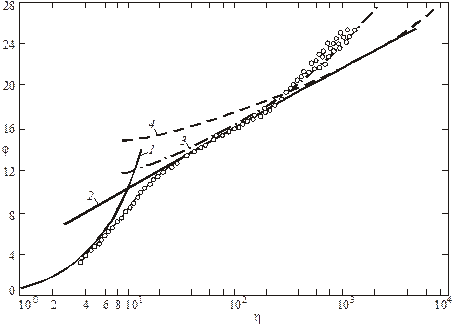
Рис. 3.11.Универсальный логарифмический закон распределения скоростей

в турбулентном пограничном слое на плоской пластине: 1 – соответствует

уравнению j = h; 2 – уравнению (3.32); 3 и 4 – степенным законам (3.49)

со значениями  n = 7 и 10 соответственно

Из сопоставления расчетов с экспериментом определяем эмпирические константы

æ = 0,4; h₁ = 11,6.                                      (3.33)

Пересечение линий 1 и 2 (см. рис. 3.11) дает расчетную толщину вязкого подслоя в двухслойной схеме пограничного слоя. Эти значения позволяют определить значение постоянной С  в формуле (3.32):

С = h₁ – (1/æ) ln h₁ = 5,5,  и окончательно формулу (3.32) можно записать в виде

j = 2,5 ln h + 5,5,                                    (3.34)

или, переходя к десятичным логарифмам,

φ = 5,75 lg η + 5,5.                                 (3.35)

Следует отметить универсальность логарифмического  профиля скорости. Его логарифмический участок сохраняется почти во всех случаях. Используя эту универсальность, метод определения коэффициента трения по измеренным профилям средней скорости, по имени его автора, называют методом Клаузера.

Логарифмический профиль скоростей практически существует почти до оси симметрии при турбулентном течении в каналах и нарушается во внешней области пограничного слоя. Формула (3.34) неприменима на большом удалении от стенки также и потому, что в ней неограниченное увеличение значения у  приводит к неограниченному росту скорости и, в то время как последняя величина при у → ∞ равна U₀. Таким образом, этой формулой следует пользоваться в рамках теории пограничного слоя конечной толщины. Отклонение истинного изотермического турбулентного профиля скоростей на пластине от логарифмического имеет место только в области значений 0,9 < ω < 1 [5].

Здесь следует отметить, что безразмерная толщина ламинарного подслоя, определенная как =11,6, практически не зависит от условий обтекания. Так, проведенный анализ показывает, что при увеличении числа Маха до М = 9 относительная толщина вязкого подслоя у₁/δ возрастает до значения у₁/δ ≈ 0,2…0,3 (при М → 0 у₁/δ ≈ 0,01), но при этом значение η не изменяется, η ~ 11,6 = = const.

Из условия η₁ = 11,6 сразу можно найти число Рейнольдса вязкого подслоя:

 

но так как φ₁ = η₁ = 11,6, то

                              (3.36)

т.е. собственное число Рейнольдса вязкого подслоя автомодельно относительно числа Рейнольдса потока в целом.

Иногда используют закон дефекта скорости в турбулентном пограничном слое, который получается из логарифмического профиля

                              (3.37)

Если действие этой зависимости распространить вплоть до внешней границы пограничного слоя, то при  у = δ, u = U₀

                            (3.38)

Вычитая почленно (3.37) из (3.38), получаем выражение для дефекта скорости

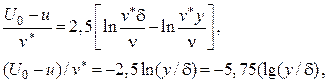                  (3.39)

или с учетом того, что

                             (3.40)

Следует иметь в виду, что значение логарифма здесь будет отрицательно (y/δ < 1).

Закон дефекта скорости (3.39) является универсальным законом, который хорошо подтверждается экспериментом (рис. 3.12).

Интересно отметить, что закон дефекта скорости в таком виде справедлив как для гладкой, так и для шероховатой поверхности, хотя распределения скорости в обычных координатах (u/U₀ = f(y/δ)) при этом значительно различаются.