Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 3

Понятно, что средние значения пульсационных величин равны нулю:

Точно так же равны нулю средние произведения  типа

В связи с этим для оценки величины турбулентных пульсаций используют их среднеквадратичные значения  При этом относительная величина пульсаций, характеризующая степень турбулентности потока, определяется как  Применительно к трехмерному течению степень турбулентности можно найти следующим образом:

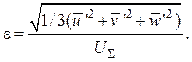                               (3.4)

Средние значения скорости, давления и  температуры представляют собой величины, измеряемые при помощи инерционных датчиков. Среднее значение пульсационных величин  как уже было сказано, равно нулю и инерционные датчики их не регистрируют. Однако следует обратить внимание на то, что средние значения произведений пульсационных составляющих могут быть не равны нулю:

В таком случае говорят, что между пульсациями существует корреляция. Появление в турбулентном потоке дополнительного механизма передачи импульса и энергии связано с существованием корреляций между пульсациями.

В дальнейшем для простоты будем опускать черту над осредненными по времени основными параметрами, обозначая их большими буквами U, V, P, T или Q, а малыми буквами u, v, p и  t  или    со штрихом или без него будем обозначать пульсации этих параметров.

На рис. 3.5 приведено распределение турбулентных пульсаций скорости в пограничном слое на пластине. Как видно, продольные пульсации примерно в два раза больше поперечных. При приближении к стенке и к внешней границе пограничного слоя их значения уменьшаются.

При турбулентном течении в потоке возникают пульсации скорости; отдельные объемы жидкости начинают двигаться поперек потока, причем эти объемы существенно больше тех, к которым можно применять понятие дифференциального объема сплошной среды. Дифференциальный объем сплошной среды – это, с одной стороны, бесконечно малая (в математическом смысле) величина, но с другой – достаточный объем (большое число молекул), чтобы можно было считать жидкость или газ сплошной средой. Следовательно, жидкость по-прежнему есть континуум, и к ней применимы общие уравнения гидродинамики.

Тогда, если в уравнение Навье – Стокса подставить истинные (мгновенные) значения скоростей в виде суммы средних и пульсационных значений и применить рассмотренные выше правила осреднения, то получим уравнения движения для осредненного течения.  Это впервые сделал Рейнольдс, поэтому дифференциальные уравнения для турбулентного движения называют уравнениями Рейнольдса.

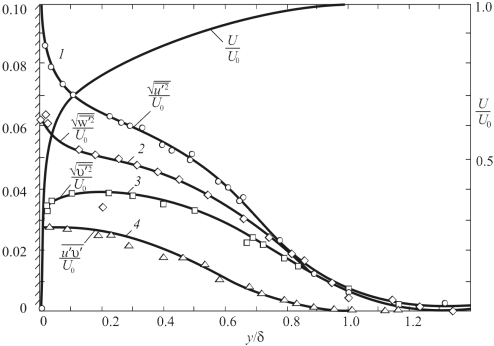
Рис. 3.5.  Распределение турбулентных пульсаций скорости

в пограничном слое на продольно обтекаемой плоской пластине.

ū – осредненная скорость, 1 –  продольные пульсации

2 – поперечные пульсации  параллельные  стенке;

3 – поперечные пульсации  перпендикулярные стенке;

4 – турбулентное касательное напряжение

Для осредненного двумерного течения несжимаемой жидкости уравнения Рейнольдса имеют вид

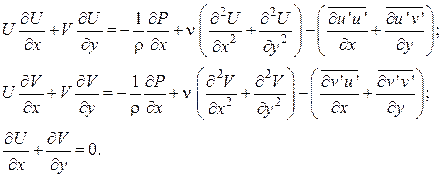(3.5)

В этих уравнениях, в отличие от уравнений для ламинарного течения (Навье – Стокса), число неизвестных (U, V, P, ) больше числа уравнений (появились новые неизвестные – корреляции ). Для замыкания  системы необходимо принять какие-то гипотезы, связывающие пульсационные составляющие скорости с их средними значениями.

Аналогично можно записать уравнения для осредненных значений температуры и концентраций, получаемые из (1.13) и (1.14) путем подстановки вместо мгновенных значений параметров Т  и С суммы их средних и пульсационных составляющих  и последующего осреднения уравнений:

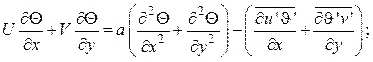           (3.6)

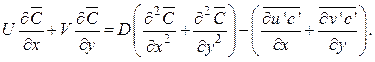            (3.7)

Уравнение (3.6) описывает распространение теплоты в турбулентном движении, а (3.7) представляет собой уравнение турбулентной диффузии вещества.

Как видно, по сравнению с исходными уравнениями (1.13) и (1.14), в них также появились дополнительные неизвестные. Это корреляции типа  которые представляют собой составляющие турбулентного потока теплоты и вещества.

3.3.  Дополнительная вязкость