Конечно, турбулентные критерии принципиально отличаются от своих ламинарных прототипов прежде всего тем, что они обусловлены формой движения, а не только физическими постоянными среды. Более того, числа Prt и Sct мало зависят от своих молекулярных аналогов. Это объясняется заложенной в основе теории турбулентного переноса идеей о том, что одни те же жидкие объемы, или «моли» жидкости, одновременно переносят импульс, теплоту и вещество. При этом можно предположить, что коэффициенты турбулентного переноса nt, at и Dt близки между собой, т.е. турбулентные числа Прандтля и Шмидта должны не слишком отличаться от единицы. Этот вывод подтверждается измерениями различных авторов.
3.4. Полуэмпирические гипотезы
для расчета турбулентных течений
Как было показано выше, дифференциальные уравнения турбулентного пограничного слоя отличаются от соответствующих дифференциальных уравнений ламинарного пограничного слоя дополнительными членами
которые можно трактовать как дополнительные «рейнольдсовы» напряжения, составляющие теплового потока и массы, возникающие за счет турбулентности. Поскольку эти величины неизвестны, система дифференциальных уравнений турбулентного пограничного слоя является незамкнутой. Для ее замыкания необходимо найти связь между пульсационными и осредненными параметрами течения. Теоретически найти такую связь пока не удалось.
Поэтому обычно принимаются гипотезы, связывающие турбулентное трение и тепловой поток с параметрами осредненного течения. Эти гипотезы, позволяющие решать задачи пограничного слоя, составляют основу полуэмпирической теории турбулентности.
Для турбулентного напряжения трения такая гипотеза была первоначально высказана Буссинеском, предложившим определять турбулентное трение выражением, аналогичным формуле Ньютона:
Необходимо, однако, иметь в виду, что турбулентная вязкость μt, в отличие от молекулярной вязкости μ, не является физической константой жидкости, а зависит от распределения скорости.
Пример изменения кинематической турбулентной вязкости приведен на рис. 3.7.
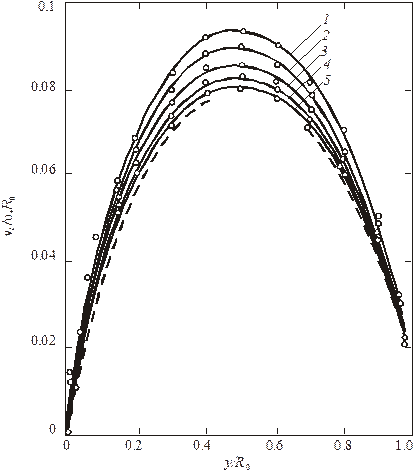
Рис. 3.7. Распределение кинематической турбулентной вязкости
по радиусу трубы в изотермическом потоке несжимаемой жидкости
по опытам Никурадзе [4]: 1 – Re = 4∙103; 2 – 9∙103; 3 – 23∙103;
4 – 43∙103; 5 – 105∙103
Для установления связи между пульсациями скорости и полем средней скорости Прандтлем была предложена гипотеза пути перемешивания. (Иногда ее называют теорией пути смешения.) Путь смешения, введенный Прандтлем, в известной мере аналогичен длине свободного пробега молекул в кинетической теории газа с той разницей, что здесь происходят макроскопические движения турбулентных масс.
Рассмотрим в параллельном потоке два слоя жидкости на расстоянии Δу. Скорости в этих слоях различны, и из-за пульсаций существует обмен импульсами между отдельными струйками.
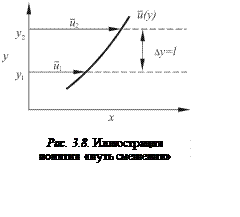Теория пути смешения основывается на
предположении, что комок жидкости, перемещающейся при пульсации из одного слоя
в другой, сохраняет составляющую импульса в направлении оси х на
некотором расстоянии l,
названном путем смешения. Если на рис. 3.8 расстояние между слоями Δу =
l, то частицы, поступающие из нижнего
слоя в верхний, сохраняют свою скорость. Разность между средней скоростью
потока в точке у2 и мгновенной скоростью поступающих сюда
частиц из нижнего слоя дает пульсацию скорости в этом месте 
но если lмало, то 
Таким образом, величина пульсации
(3.16)
Пульсации в поперечном и продольном направлениях связаны между собой, v ~ и¢. Окончательно с точностью до некоторого коэффициента пропорциональности, который можно включить в l, получим для турбулентного напряжения трения
(3.17)
Для последнего выражения будет более правильным следующий вид:
(3.18)
так как знак касательного напряжения определяется знаком производной. Тогда турбулентную вязкость можно выразить как
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.