Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 6

                                           (3.19)

Такие же рассуждения могут быть использованы и при переносе теплоты и вещества. В результате получим

                   (3.20)

                    (3.21)

В общем случае значения l, l_т и l_д могут быть не равны, и соответственно коэффициенты турбулентного обмена μ_t, λ_t и D_t будут отличаться.

В зависимостях (3.20) и (3.21) вместо неизвестных значений пульсаций  введена новая неизвестная l. Во многих случаях посредством введения различных гипотез удается установить связь между l и характерной геометрией течения. Одна из таких гипотез – гипотеза Прандтля, – как будет показано ниже, оказалась весьма эффективной при расчете осредненных параметров турбулентного пограничного слоя.

3.5.   Логарифмические и степенные профили

         скорости, законы трения

          и тепломассообмена

3.5.1. Логарифмический закон распределения

          скоростей

Из формулы Прандтля (3.17) для турбулентного трения выводится универсальный логарифмический закон распределения скорости в турбулентном пограничном слое. При турбулентном режиме течения общее напряжение трения складывается из трения, вызванного молекулярной вязкостью, и турбулентного трения, вызванного пульсациями:

                      (3.22)

На большом расстоянии от стенки значение турбулентной вязкости намного превышает молекулярную вязкость μ_t > μ. Область пограничного слоя, в которой можно пренебречь молекулярной вязкостью, называется турбулентным ядром.  Вблизи стенки турбулентные пульсации затухают и молекулярная вязкость играет решающую роль. Эта часть пограничного слоя называется ламинарным подслоем (рис. 3.9). Его толщина у₁ = δ_л составляет 1–2 % от общей толщины слоя при течении несжимаемой жидкости. Между ними находится переходная область, в которой значения молекулярной и турбулентной вязкости одного порядка.

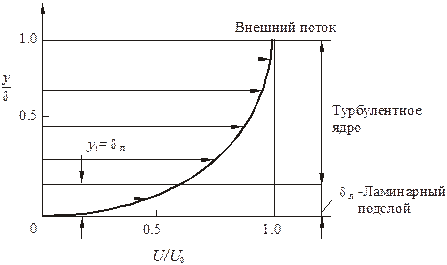
Рис. 3.9.  Двухслойная модель пограничного слоя

В общем случае, если рассматривать трехслойную схему течения, для переходной области получают громоздкие и неудобные для дальнейшего анализа соотношения. Практически достаточно рассмотреть двухслойную схему турбулентного пограничного слоя, состоящую из ламинарного подслоя и турбулентного ядра.

В области вязкого подслоя при y< y₁, τ >> τ_t

                                           (3.23)

если принять во внимание, что y₁ << δ, то в области подслоя τ → τ_ст, что соответствует линейному профилю скорости. На рис. 3.10 показано распределение касательных напряжений по толщине пограничного слоя.

Введя обозначения

          (3.24)

где v^* – так называемая динамическая скорость (скорость трения), представим соотношение (3.23) в безразмерной форме

или с учетом того, что в вязком подслое τ → τ_ст,

                                 (3.25)

т.е. получим линейное распределение скорости.

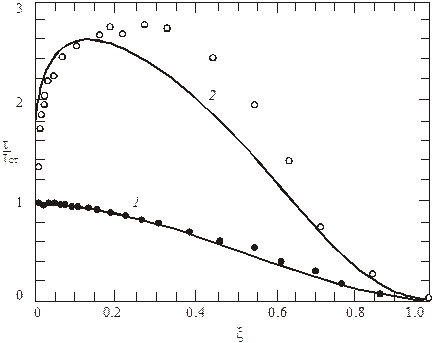
Рис. 3.10. Распределение касательного напряжения трения

по сечению пограничного слоя:   1 – τ / τ_ст = 1 – 3ξ² + 2 ξ³,

 (●)  –  экспериментальные  точки в пограничном слое без вдува,

j_ст = 0; 2 – τ / τ_ст = (τ ₀/ τ_ст) (1 + b₁ω), (○) – деформация профиля

при вдуве,  j_ст = 0,003; b = 1,3; Ψ = 0,456

Вообще-то это условие можно было сразу принять ввиду малой толщины вязкого подслоя по сравнению с толщиной всего пограничного слоя: y₁ << δ.

В области турбулентного ядра «ламинарное» трение τ_л незначительно по сравнению с «турбулентным» (τ_t >> τ_л) и поэтому можно считать τ = τ_t, т.е.

                                  (3.26)

Путь перемешивания l на стенке должен быть равен нулю, так как на ней пульсационное движение исчезает. В первом приближении его можно принять пропорциональным расстоянию от стенки

l = æу,                                                (3.27)

где æ – безразмерная постоянная, которая должна быть определена из опыта.

Кроме  того,  в   области   турбулентного ядра, близкой к стенке, при  у₁ << y << δ также принимаем

τ = τ_t ~ τ_ст.                                            (3.28)