34
Обратимся теперь к зависимости (2.1) и конкретизируем се применительно к характеристикам моделируемых объектов, полагая, что связи между их входами и выходами линейны. Для таких преобразователей формула (2.1) записывается в виде
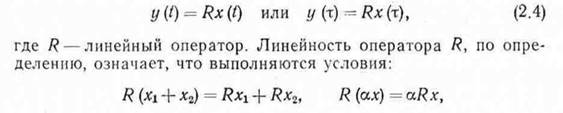
где х, JCi, Xz—любые функции или последовательности, к которым применим оператор R; а.—любое действительное число. Линейными являются операторы дифференцирования, интегрирования и оператор, соответствующий последовательному применению различных линейных операторов. Примером нелинейного оператора является иозведепне в степень.
Динамическая модель экономического объекта может рассматриваться как структурно-функциональная, так как в ней находят отражение его структура и способ функционирования.
При изучении экономической системы часто предполагают, что ее реакция на входные воздействия реализуется «мгновенно», т. е. пренебрегают фактически существующими в любой реальной системе запаздываниями между входом и выходом. В таких случаях динамическая модель трактуется как безынерционная. Подобную модель мы будем в дальнейшем называть кинематической. Кинематическая модель1 описывает зависимость между траекториями се входа и выхода в виде
![]()
Следует подчеркнуть, что кинематическая модель отличается от динамической тем, что переходные процессы в системе, обусловленные ее инерционными и демпфирующими характеристиками, не учитываются. Образно говоря, в кинематических моделях внутренняя структура «черного ящика», в качестве которой выступает объект моделирования, по существу, остается нераскрытой. Поэтому в информационном отношении они менее содержательны, чем динамические модели.
Упомянем, наконец, модели, описывающие зависимости между входами и выходами преобразователя в предположении, что он пребывает в состоянии «покоя» (равновесия). Такие модели называют статическими, и они формируются в виде алгебраических соотношений, в которых значения входных и выходных величин принимаются независимыми от времени. Ста33
тическая модель описывает состояние объекта в некоторый фиксированный момент времени вне связи с его состояниями в другие моменты. Примером такой модели является статический межотраслевой баланс.
В практике экономических исследований наряду с описанными используются и другие средства моделирования: модели с конкретными числовыми значениями характеристик (их называют числовыми), записанные с помощью логических выражений, представленные в графических образах (диаграммы, графики, рисунки, чертежи). К логическим моделям обычно относятся блок-схема алгоритмов и программы расчетов на ЭВМ. Модели, реализованные на ЭВМ, называют также машинными. Модели, предназначенные для объяснения наблюдаемых факторов или прогноза поведения объекта, называются дескриптивными. Они отвечают на вопросы «как это происходит, как будет развиваться?» Модели, предназначенные для определения наилучшего или допустимого с точки зрения исследователя состояния объекта, называются нормативными. Они отвечают на вопрос «как должно быть?» и могут использоваться для сравнения нормативного состояния с действительностью.
Современное состояние и дальнейшее развитие моделирования экономических процессов особенно тесно связаны с комплексом математических или, как чаще говорят, экономико-математических моделей. На нем во всевозрастающей мере основываются анализ и планирование экономических процессов, разработка эффективных методов управления, наконец, автоматизация планово-экономических расчетов. Точность и обоснованность анализа и управления зависят от объективности и точности отражения в моделях реальных экономических процессов, связей между параметрами экономической системы, ограничений, накладываемых на нее внешними условиями, достоверности используемой информации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.