Экономическая система как объект экономической кибернетики (Часть учебного пособия "Экономическая кибернетика"), страница 2

32

и тем же поведением (в пределах точности его наблюдений) J,j. могут обладать системы различной структуры и физической природы.

Рассмотрим две системы А и В с векторами входов –xa,хia, х2а, ..., ХтА и Лв^в, ^2В, ..., -Утв) и векторами выходов уа(</!а, У2А, ..., УпА) И УвО/1В, У2В, ..., Упв) СООТВСТСТВСННО.

Говорят, что системы А и В изоморфны, если

При X^(t)=X^{t), ^2В 0 =^2А 0, . . ., X^{t)=X^(t) для любого момента времени. Изоморфные системы неотличимы друг от друга для наблюдателя, следящего только за их входами и выходами. Поведение данной системы ничем не отличается от поведения всех изоморфных ей систем, и любая из совокупности таких систем может рассматриваться как оригинал или модель остальных.

Изоморфны схема на рис. 2.2 и система уравнений (2.2). Можно построить изоморфные им механическую или электрическую системы, поведение которых будет описываться той же системой уравнений (2.2).

Наличие изоморфизма не является необходимым условием соответствия модели оригиналу. Система В может служить моделью поведения системы А также и тогда, когда их сходство не столь полно, как это требуют условия (2.3). Частным важным соотношением «оригинал — модель» является отношение гомоморфизма, при котором существует однозначное соответствие между состоянием систем Л и В и неоднозначно-обратное соответствие. Так система. В полученная из системы А, при ее упрощении (за счет уменьшения числа рассматриваемых переменных путем их объединения), является гомоморфной моделью системы А. Иначе говоря, пользуясь системой В как гомоморфной моделью системы Л, мы можем не «различить» некоторые состояния системы А, для нас они как бы сольются в одно.

Для иллюстрации этих положений обратимся к примеру. Пусть функционирование двух систем А и В описывается следующими моделями, заданными таблицами переходов для состояний систем:

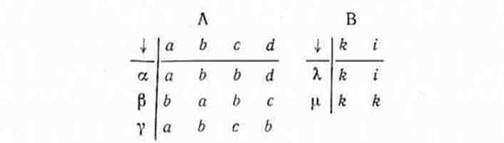
Здесь верхние строки задают исходные состояния, а крайние левые столбцы — операторы, при воздействии которых система переходит из одного состояния в другое. Так, в системе А воздействие оператора <х на исходное состояние с переводит ее в состояние Ь. Аналогично в системе В воздействие оператора Х на состояние i не изменяет его, а воздействие оператора u на то же состояние переводит систему в состояние k.

Покажем, что системы А и В гомоморфны, т. с. что существует односторонне-однозначное преобразование, которое переполиi элементы системы А в элементы системы В; обратный процесс нсрсализусм.

Для этого построим следующий оператор преобразования, переводящий состояния и операторы системы А в состояния и операторы системы В.

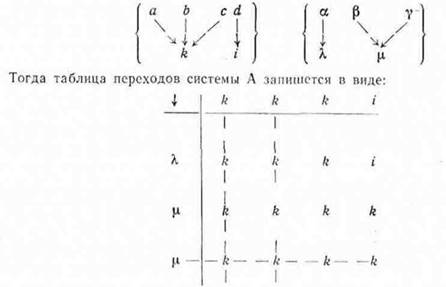
Нетрудно установить, что после вычеркивания повторяющихся строк н столбцов она в точности воспроизводит 1аблнцу переходов системы В.

Заметим, что гомоморфными являются также системы, образованные детализированными совокупностями ресурсов и агрегатами, построенными путем их укрупнения. Аналогичное положение имеет место при агрегировании продукции (см. 12.2).

Математическое моделирование. В математических моделях используются символы (буквы, цифры, математические знаки) и их последовательности (формулы, уравнения, неравенства), с помощью которых описываются изучаемые свойства оригинала. Математическая модель, претендующая на роль эффективного инструмента при изучении экономических процессов (экономико-математическая модель), должна отвечать следующим общим требованиям: а) строиться на базе экономической теории и отражать объективные закономерности процессов; б) правильно отображать функцию и (или) структуру данной реальной экономической системы; в) удовлетворять определенным математическим условиям (разрешимость, согласованность размерностей и т. д.).

Примем в качестве оригинала некоторый материальный объект (систему, преобразователь), полагая, что он имеет один вход и один выход и преобразует материальные или информационные потоки. В общем случае вход и ш.1\од—суть непрерывные или дискретные функции времени и для описания их взаимосвязей будем пользоваться соответственно непрерывными и дискретными моделями.