Нелинейное волновое уравнение для комплексного вектор-потенциала

УДК 538.3

НЕЛИНЕЙНОЕ ВОЛНОВОЕ УРАВНЕНИЕ ДЛЯ КОМПЛЕКСНОГО  ВЕКТОР-ПОТЕНЦИАЛА

Томск, Сибирский физико-технический институт,

Для совместного описания электромагнитных и гравитационных явлений предлагается использовать нелинейное волновое уравнение для четырёхмерного комплексного потенциала. Уравнение инвариантно относительно лоренцевых и калибровочных преобразований. Вектор тока, играющий роль источника комплексного поля, представлен как результат свёртки тензора энергии-импульса этого поля с векторами четырёхмерной скорости движения полюсов поля. Получены строгие и численные решения для стационарного случая и рассмотрено взаимодействие этих решений.

ВВЕДЕНИЕ

Уравнения Максвелла представляют собой обобщение законов электромагнетизма. Все попытки дальнейшего обобщения этих уравнений оказывались безуспешными. Тем не мене эти попытки не прекращаются до сих пор. Можно отметить, по крайней мере, два момента стимулирующих эти поиски. Уравнения Максвелла содержат «чуждые» элементы: заряды и токи. Г. Ми [1] предполагал, что электрические заряды представляют собой сгустки электромагнитного поля. Поиски полевых моделей элементарных частиц предпринимались и другими учёными, но все они оказывались безрезультатными. О. Хевисайд [2] указывал на сходство законов гравитации и электромагнетизма. Это сходство позволяет предположить, что гравитационные и электромагнитные поля имеют общую природу и поэтому могут быть описаны общими уравнениями. На необходимость возврата гравитации статуса физического поля указывал в своей последней работе Л. Бриллюэн [3]. Предлагаемую работу можно рассматривать как развитие высказанных Бриллюэном идей.

НЕЛИНЕЙНОЕ КОМПЛЕКСНОЕ ВОЛНОВОЕ УРАВНЕНИЕ

            В настоящей работе в качестве первичного понятия предлагается использовать комплексный 4-потенциал A=(j,A), определенный как 4-вектор в пространстве Минковского. Постулируется, что поведение этого 4-вектора  описывается следующим нелинейным дифференциальным уравнением:

где x^k =(ct, x) - четырёхмерные  пространственно-временные координаты, i в правой части - мнимая единица, компоненты четырехмерного вектора u_j определяются трёхмерным  вектором скорости v посредством соотношений

в качестве единицы скорости выбрана скорость света,  T  ^ij - тензор второго ранга, определяемый через производные  от  A следующим образом:

Здесь  g^ik - метрический тензор пространства Минковского; как общепринято, по повторяющимся индексам ведётся суммирование; поднятие и опускание индексов производится стандартно с помощью метрического тензора. Для удобства здесь и далее все выражения, если не делается специальных оговорок,  записываются в безразмерных единицах.

Дополнительно на потенциал A налагаются калибровочные условия Лоренца:

Роль наблюдаемых играют напряженности комплексных электрического (E) и магнитного (H) полей, определяемых известными соотношениями:

Переход от комплексных  векторов E и H к реальным полям осуществляется согласно соотношениям E=E_e +i E_g и H=H_e +i H_g , где индексы e и g указывают на электромагнитную или гравитационную природу полей, соответственно.

Таким образом, всё обобщение уравнений Максвелла свелось к  замене реального выражения  4pj^k , представляющего внешний источник электромагнитного поля, комплексным выражением iu_jT^kj , согласно которому внешние источники устраняются путём замены их нелинейным по комплексному полю выражением. Кроме того, областью значений компонент вектора потенциала вместо вещественной оси становится вся комплексная плоскость.

Выражения (1 - 4) составляют основу предлагаемого математического формализма теории комплексных полей. Однако превращение этих основ в завершенную теорию возможно лишь в случае, если удастся показать адекватность физической картины мира модельной, следующей из предложенной теории. Для этого надо показать, что основные физические законы могут быть выведены из волнового уравнения (1) и, что это уравнение допускает решения в виде сгустков полей, которые могут рассматриваться в качестве моделей  элементарных частиц. Разумеется, решение этой задачи в полном объёме по силам лишь большим научным коллективам. Цель автора скромнее: на отдельных примерах показать перспективность этого направления исследований.

УРАВНЕНИЕ НЕПРЕРЫВНОСТИ ПЛОТНОСТИ КОМПЛЕКСНОГО ЗАРЯДА

Как указывалось выше, величина iu_jT^kj, представляющие собой 4-вектор плотности комплексного тока j^k. Нулевая компонента этого тока соответствует плотности  комплексного заряда r=r_e+i r_g, а три остальных представляют  трехмерный вектор плотности комплексного тока j=j_e +i j_g. Подставляя в выражения (2) для компонент тензора T ^kj соответствующие компоненты комплексных полей и проводя суммирование по повторяющимся индексам, легко получить следующие выражения для плотности комплексного заряда и тока:

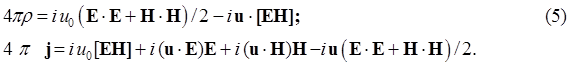Наблюдается асимметрия в условиях существовании источников электромагнитных и гравитационных полей. Существование  источников электромагнитных полей невозможно в отсутствии одного из видов этих полей. Тогда как возможно автономное существование гравитационных полей при отсутствии электромагнитного поля. Плотность гравитационного заряда в этом случае будет отрицательной (для u₀>0).