Нелинейное волновое уравнение для комплексного вектор-потенциала, страница 6

Различие масс у электрона и протона в рамках этой модели объясняется тем, что из-за большего значения магнитного момента у электрона его комплексное электрическое поле раньше, чем у протона, становится почти полностью реальным (E_e=|E|cos(j), E_g=|E|sin(j)).  Как следует из точного решения без учёта магнитного поля радиус сферы, на поверхности которой фаза комплексного поля E обращается в ноль, определяется отношением  r=(m²+e²)/2m. Если этим выражением воспользоваться для оценки масс при наличии магнитного поля, то массы электрона и протона согласно расчётам фаз, представленных на рис.5, окажутся в ~5 раз меньше реальных, но отношение масс сохранится с точностью ~10%.

При решении уравнений (15), кроме проблем, связанных с ограничениями компьютерных возможностей, имели место проблемы принципиального характера. Для этих уравнений могут быть найдены асимптотические решения в окрестности 0 и на бесконечности. Эти решения удавалось «сшивать» путём введения в правую часть уравнения (15) для потенциала A_j. дополнительного члена, подобного току смещения. Это означает, что полевые образования, с отличным от нуля вектор-потенциалом A, наряду со стационарной компонентой, должны обладать осциллирующим членом. Возможно, здесь кроется разгадка связи частоты осцилляций с энергией. Однако рассмотрение нестационарных задач выходит за рамки настоящей работы.

ВЗАИМОДЕЙСТВИЕ ПОЛЕВЫХ ОБРАЗОВАНИЙ

Рассмотренные выше полевые образования соответствуют стационарному случаю при условии, если они представлены в единственном числе. Для суперпозиции нескольких образований условие стационарности нарушается. При этом изменяться со временем могут положения полюсов каждого из образований r_a и скорости их движения v_a. Волновое уравнение (1) описывает комплексное поле, обладающее одним полюсом. В общем случае правая часть волнового уравнения должна учитывать все полюсы комплексного поля. Для этого выражения (5) для плотности комплексного заряда и тока должны быть заменены следующими:

Здесь полное поле системы, состоящее из полей каждого из полюсов и поля "излучения", которое появляется в результате взаимодействия полевых образований.

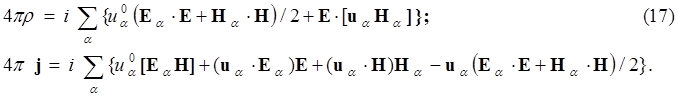Смысл выражений (17)  достаточно прозрачен. Например, интеграл от реальной части выражения в фигурных скобках для плотности комплексного заряда представляет собой  полную собственную для данного полюса энергию электромагнитного и гравитационного полей и энергию взаимодействия собственного поля данного полюса с полем других полюсов и полем излучения. Интеграл от мнимой части равен собственному электрическому заряду полюса плюс наводимый заряд за счёт взаимодействия с другими полюсами.

            Если полевые образования взаимно удалены друг от друга так, что расстояния между ними существенно превосходят радиус сфер, в пределах которых сосредоточен заряд каждого из них, то закон сохранения полного комплексного заряда принимает вид

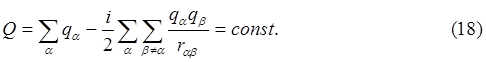Здесь r_ab- расстояние между полюсами a и b (в общем случае должно определяться с учётом запаздывания.

Комплексное выражение (18) представляет собой два закона: закон сохранения энергии и закон сохранения электрического заряда. Получено оно путем интегрирования по всему пространству комплексной плотности заряда, определяемой выражением (5) при отсутствии комплексного магнитного поля H. Вкладом в интеграл членов, включающих излучение, пренебрегалось. Интеграл вычислялся по частям в предположении постоянства потенциала каждого из образований в окрестности полюсов остальных образований. Размеры этой окрестности брались такими, чтобы интеграл собственной плотности комплексного заряда r_a с высокой точностью равнялся q_{. Ý}тому условию соответствует неравенство |q_a| «r_ab.