Нелинейное волновое уравнение для комплексного вектор-потенциала, страница 3

Как следует из этих выражений, при любых значениях постоянной интегрирования у напряженности электрического поля особенности отсутствуют. У гравитационного поля существует только одна особенность в начале координат типа r^-1, других же особенностей, указывающих на наличие гравитационного радиуса, нет. Кроме того, гравитационное поле внутри сферы r=g имеет противоположный относительно внешнего поля знак. Следовательно, здесь гравитационное притяжение сменяется отталкиванием. Это ещё один аргумент против гравитационного коллапса.

Рис.1

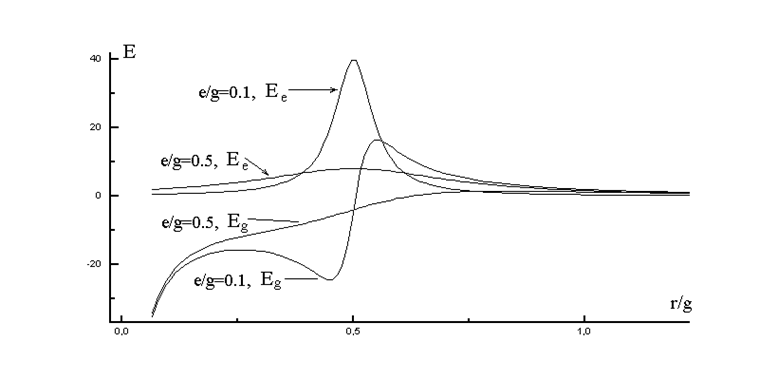На рис.1 в безразмерных величинах представлены кривые напряженности электрического и гравитационного полей для двух значений электрического заряда: e=0.1 и e=0.5. Значение гравитационного заряда g=1. Как видно из рисунка, электрическое поле концентрируется в пределах сферического слоя толщиной e, а максимум этого поля находится на поверхности сферы с радиусом g/2. В пределах сферы радиуса g знак гравитационного поля отрицательный, а вне сферы положительный.

            При больших r (r>>g) абсолютные значения реальной и мнимой компонент поля убывают по закону Кулона, поэтому значения e и g могут рассматриваться как электрический и гравитационный заряды, соответственно. Чтобы убедиться, что это действительно так, следует произвести интегрирование по всему пространству плотности электрического и гравитационного зарядов, определённых выражениями (5). В результате интегрирования легко получить

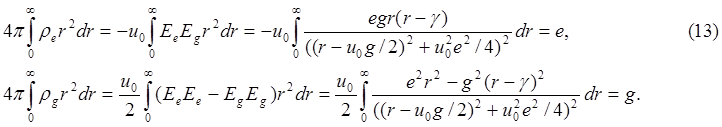Самое интересное в этих выражениях то,  что не смотря на сложную зависимость подынтегральных функций от обеих компонент комплексного заряда, результат интегрирования зависит лишь от одной компоненты: в первом интеграле от  e, а во втором  от g. Второй интеграл представляет известное соотношение: E=mc². Действительно, в левой части этого выражения стоит интеграл от суммы плотности энергии гравитационного и электрического полей, а в правой части гравитационный заряд g. Следовательно, g=E. Соотношение g=E более конкретно, чем E=mc² , поскольку в нём раскрывается смыл понятия энергии, тогда как в последнем соотношении под E понимается вся энергия, содержащаяся в частице с массой m. Не уточняется: где и в каком виде локализована эта энергия. Здесь же чётко показано, что гравитационный заряд (гравитационная масса) определяется интегралом по всему пространству от плотности энергии гравитационного и электрического полей.

Первое из соотношений (13) не мене интересно, чем второе. В нём впервые электрический заряд из категории первичных понятий, переходит во вторичные. Показано, что роль электрического заряда играет величина, равная интегралу от скалярного произведения векторов напряженности электрического и  гравитационного полей.

В компактном виде два вещественных выражения (13) можно представить одним соотношением между значениями комплексным заряда  q=e+ig и интегралом  "комплексной  энергии" W: q=iu₀W. В свою очередь W определяется интегралом по всему пространству плотности комплексной энергии. Поле, представленное на рис.1, соответствует случаю, когда значение реальной части этого интеграла положительно. Если g<0, то интеграл энергии гравитационного поля по абсолютной величине будет превосходить интеграл энергии электрического поля. Соответствующая такому полевому образованию частица будет иметь отрицательную массу.

Рис.2

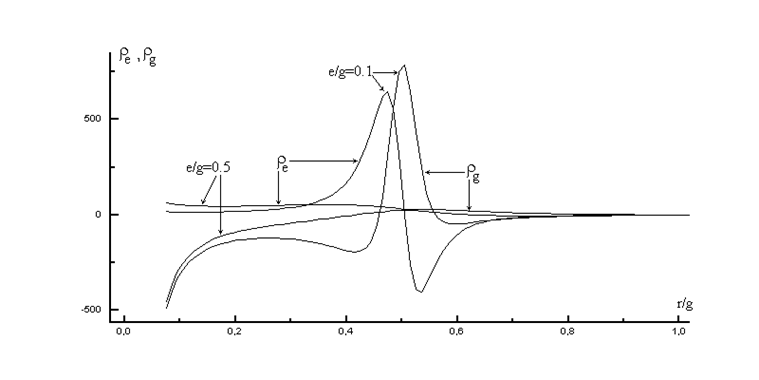На рис.2 в качестве примера приведены кривые для плотности электрического и гравитационного зарядов. Интегральные значения зарядов брались те же, что и на Рис.1.