Из волнового уравнения с учётом калибровочных соотношений (3) следует уравнение непрерывности комплексного заряда:
Согласно (5) плотности комплексного заряда можно представить суммой из двух слагаемых:
одно из которых можно определить как плотность "собственной" комплексной энергии полевого образования, а второе как плотность его "кинетической" энергии. Действительно, второй член в выражении (5) для r обращается в ноль для покоящегося полевого образования (u=0).То, что областью значений r является вся комплексная плоскость, вместо привычной положительной вещественной оси, не должно смущать. Реальная часть этой величины представляет собой плотность электрического заряда и, соответственно, может иметь любой знак. Мнимая часть является плотностью гравитационного заряда, которая может принимать отрицательные значения, если сумма квадратов векторов Eg и Hg, представляющих гравитационное поле, превосходит соответствующую электромагнитному полю сумму. То, что традиционная физика не предусматривает такой ситуации, ещё не означает отсутствие её в реальном мире. Ниже будет показано, что устойчивые полевые образования, представляющие решения волнового уравнения (1), содержат внутри себя область, где Real(U)<0.
Наряду с уравнением непрерывности (6) волновое уравнение позволяет получить закон изменения собственной энергии комплексного поля, который можно записать в следующем виде:
Из (6) и (7) следует уравнение, определяющее изменение плотности кинетической энергии
Предыдущие выкладки, хотя и позволяют с новой стороны взглянуть на известные явления, могут выглядеть как своего рода математическая манипуляция, если на конкретных решениях волнового уравнения (1) не будет показано, что источники, определяемые выражениями (5), подобны источникам реально наблюдаемых электромагнитных и гравитационных полей. В настоящее время строго решить задачу в общей постановке не представляется возможным. Однако для некоторых простых ситуаций решение может быть найдено, и найдено строго.
Самую простую ситуацию представляет стационарный случай, когда трехмерный комплексный вектор-потенциал A равен нулю. В этом случае выражение (2) сводится к одному нелинейному уравнению для комплексного потенциала j :
Соответствующее выражение для трехмерного комплексного вектора E имеет вид
Здесь Êr - радиальная компонента напряженности комплексного поля, r - радиус вектор, q=e+ig - комплексная постоянная интегрирования.
Бриллюэн [3] приводит решение этого уравнения в следующем виде Eg=a/r(r-a).
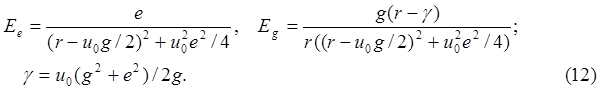 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.