Как уже говорилось, при больших r (r>>g) реальная и мнимая компоненты напряженности комплексного поля изменяются по закону Кулона. При r≤~g характер изменения напряженности поля совершенно не соответствует этому закону. В окрестности начала координат существует несколько характерных расстояний, определяющих поведение компонент комплексного поля и комплексной плотности заряда Согласно выражению (12) можно выделить три характерных размера: g, |g|/2 и |q|/2. При r <g напряжённость гравитационного поля имеет отрицательный знак. Соответственно в этой области знак плотности электрического заряда совпадает со знаком электрического заряда e. Далее следует слой, экранирующий электрический заряд.
Напряжённость электрического поля при изменении r от 0 до |g|/2 меняется от 4e/(e2 +g2) до 4/e. Т.е. по абсолютной величине возрастает. При r >|g|/2 возрастание сменяется падением, темп которого увеличивается, асимптотически приближаясь к закону Кулона.
У элементарных частиц отношение |g/e|<<1, поэтому их электрические и гравитационные поля существенно отличаются от приведенных на рисунках. Ниже на рис.3 в логарифмическом масштабе представлены значения абсолютных значений напряженности электрического и гравитационного полей, рассчитанные согласно (12) при значениях электрического заряда и массы электрона и протона.
Расчёты кривых на рисунках 1 и 2 проводились для случая, когда u0=1 и v=0. Ковариантность уравнения (2) относительно преобразований Лоренца наряду с непод
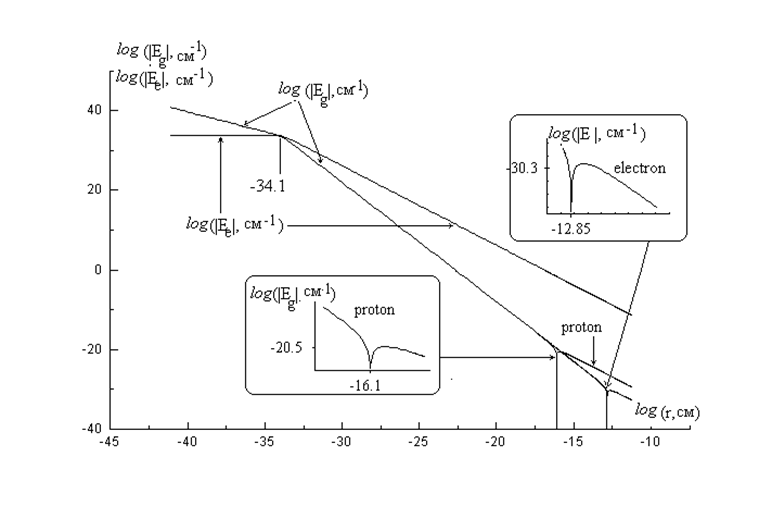 |
Рис.3
Выше рассматривались решения, для которых вектор скорости u принадлежал конусу будущего (u0>0). Выражения (12) при u0<0 представляют антиобразования, аналог антивещества. В силу различия знаков гравитационных полей антивещество должно отталкиваться от вещества, поэтому столкновение вещества с антивеществом в больших количествах происходить не могут.
Учитывая, что пространственные размеры полевых образований и значения напряженности поля изменяются в широком динамическом диапазоне (десятки порядков), желательно от системы уравнений в частных производных перейти к системе обыкновенных дифференциальных уравнений. Для этого производятся следующие допущения. Предполагается, что напряженность E незначительно отличается от сферически симметричного поля. Поскольку для поля H такое допущение сделать нельзя, то величина H×H в выражении (14) заменяется усредненным по поверхности сферы значением < H×H>. Далее полагается, что тороидальная компонента вектор-потенциала осесимметрична, и может быть представлена в следующем виде Aj=A(r)sin(q).
При этих предположениях уравнения (14) превращаются в систему обыкновенных дифференциальных уравнений для радиальной компоненты поля Er и потенциала A(r):
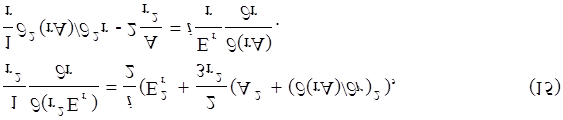 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.