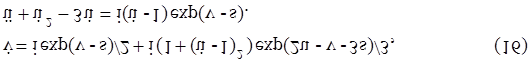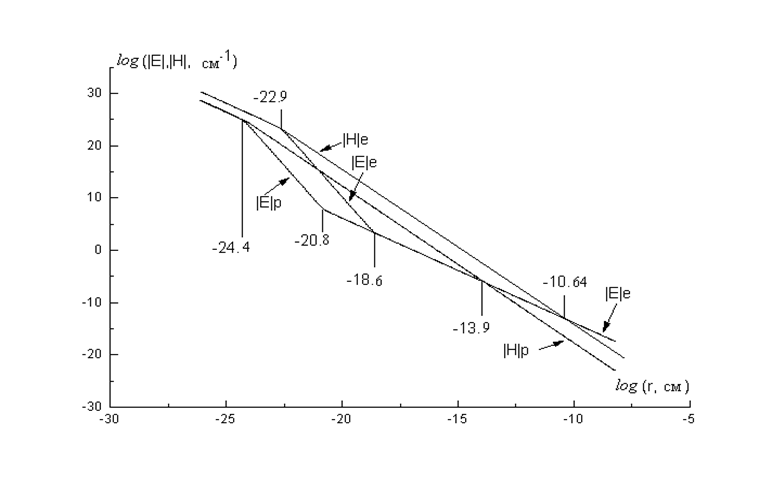Нелинейное волновое уравнение для комплексного вектор-потенциала, страница 5

            Согласно этой замене уравнения (15) трансформируются в следующие:

Здесь точка над символом означает производную по s.

Рис.4

На рис. 4 и рис.5 в полярной системе координат E_r =|E_r |exp(ij_E), <H>=|H|exp(ij_H) приведены результаты расчёта комплексного поля для значений магнитного и углового моментов, значений электрического заряда и массы, соответствующих электрону и протону.На рис.4 около характерных точек кривых модуля напряжённости комплексных электрического и магнитного полей проставлены значения log(r, см). В качестве таких точек выбраны точки пересечения кривых, соответствующих магнитному и электрическому полю, а также точки, в которых изменяется закон поведения этих полей.

Рис.5

Для модели электрона модуль напряженности магнитного поля равняется модулю напряжённости электрического поля при log(r)= -10.64. Для модели протона log(r)= -13.9. Этим расстояниям соответствуют величины близкие значениям Комптоновской длины волны электрона и протона, соответственно. Как видно из рис. 4 модуль напряжённости комплексного электрического поля изменяется по закону Кулона, начиная со значений log(r)=-18.6 для электрона и log(r)=-20.8 для протона.

Вместе с тем существует сферический слой, в пределах которого модуль напряженности электрического поля убывает пропорционально 5-степени радиуса. Для протона этот слой определяется условием  -24.5<log(r)<-20.8, а для электрона   -22.9<log(r)<-18.6. Внутренний радиус этого слоя можно оценить соотношением r_i~Öm/4, где m - магнитный момент частицы. Модуль напряженности магнитного поля, начиная с r_i~Öm/4, убывает с ростом расстояния по кубическому закону. В окрестности r_i значение модуля напряженности магнитного поля становится равным модулю напряжённости электрического поля, и это равенство выполняется в пределах некоторого слоя, где обе эти величины изменяются обратно пропорционально квадрату расстояния, т.е. по закону Кулона. К сожалению, ограничения компьютера по динамическому диапазону чисел не позволили производить расчеты для значений log(r)<-30.

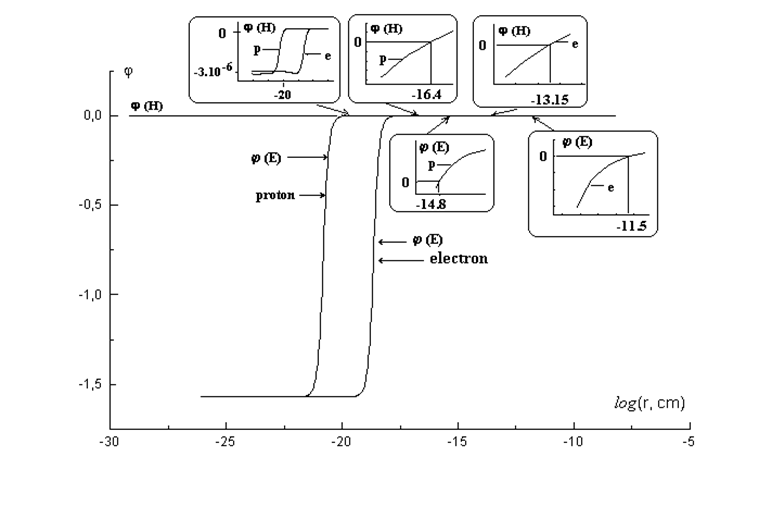
Не менее интересно ведет себя фаза комплексных полей, представленная на    рис. 5. На больших расстояниях фаза электрического поля равна фазе магнитного поля, а её значение равно отношению m/e. Для электрона m/e@4.9×10^-22, а для протона m/e@9×10^-19. Значение фазы уменьшается по мере уменьшения радиуса. Причём, темпы уменьшения у электрического и магнитного полей различны. Сначала в ноль обращается фаза электрического поля. Для электрона это происходит при  log(r)=-11.5, а для протона - при  log(r)=-14.8. В окрестности этой точки у комплексного электрического поля только реальная компонента отлична от нуля, а мнимая, представляющая гравитационное поле, обращается в ноль.

Для магнитного поля эта ситуация происходит при меньших значениях радиуса: для электрона при  log(r)=-13.15, для протона при  log(r)=-16.6. Самое интересное, что на протяжении всего расчётного участка траектории фаза магнитного поля остаётся близкой к нулю. После изменения знака фаза принимает свое минимальное значение~-3×10^-6 при  log(r)~-18.5 для электрона и при  log(r)~ -21 для протона. Таким образом, у комплексного магнитного поля во всём исследованном диапазоне расстояний значение реальной части, существенно превосходит значение мнимой части магнитного поля (гравитационного магнитного поля). Это означает, что плотность энергии комплексного магнитного поля всегда положительна.

Этого нельзя сказать о плотности энергии комплексного электрического поля. Оказывается, что при малых радиусах разность фаз магнитного и электрического поля с высокой степенью точности близка к p/2. В области, где модуль магнитного поля равен модулю электрического поля, из-за разности  фаз полей p/2 плотность энергии комплексного поля (плотность комплексного заряда) обращается в ноль.