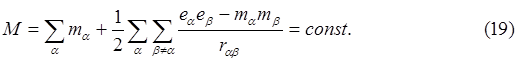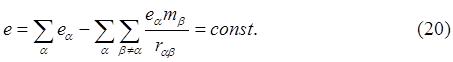Нелинейное волновое уравнение для комплексного вектор-потенциала, страница 7

                        Из закона сохранения полного комплексного заряда следует, что собственные заряды частиц q_a в процессе взаимодействия будут изменяться. Как показано выше, для одного полевого образования мнимая часть заряда равна полной энергии  поля, т.е. g_a=m_a. В случае, когда радиационными потерями можно пренебречь для системы взаимодействующих полевых образований, мнимая часть закона сохранения (18) может быть записана в следующем виде:

            Реальная часть выражения (18) представляет собой закон сохранения полного электрического заряда системы

Обычно считается, что значения собственных электрических зарядов у взаимодействующих частиц не изменяются. Члены, соответствующие обмену электрическими зарядами в выражении (20), по абсолютной величине меньше энергии кулоновского взаимодействия в  ~|e_a|/m_a раз. Для известных электрически заряженных частиц это отношение ~10²⁰. Поэтому, если изменение масс взаимодействующих частиц поддаётся наблюдению, то  обнаружение изменения электрического заряда в лабораторных условиях требует экспериментально недостижимой точности. Однако в сильных гравитационных полях  изменение собственного электрического заряда может быть заметным. Так уже на поверхности Солнца относительное изменение электрического заряда будет ~10 ^-6. На поверхности более компактных, чем Солнце, объектов это изменение имеет большие значения.

СИСТЕМА ЕДИНИЦ

Ещё в начале века  Г. Ми отмечал возможность упрощения систем единиц, если механические величины выразить через соответствующие электрические. В качестве основных размерных величин он предлагал использовать электрический заряд и электрический потенциал [1]

Использование волнового уравнения (2) для описания электромагнитных и гравитационных явлений позволяет размерность всех используемых величин определить посредством одной размерной величины.  В качестве такой величины удобно брать какой-либо характерный размер полевого образования [L]. Если потенциал представляется в безразмерных величинах, то согласно (3) размерностью напряженности поля будет [L]^-1. Соответственно размерность плотности электрического и гравитационного зарядов будет [L]^-2, а размерность заряда - [L] Переход к общепринятым единицам измерения можно осуществить, используя значения гравитационной постоянной и скорости света. Пусть для определённости эта система единиц называется электро-гравитационной (ЭГ).  Ниже приводится таблица размерности и переводных множителей основных единиц измерения.

Таблица 1

	ЭГ	множитель перевода	CGS, эл.стат. ед
Время	1 см	с-1	0.333 10-10 сек
Масса	1 см	с2/G	1.348 1028 г
Электрический заряд	1 см	c2/G1/2	3.48 1024 эл.ст.ед
Напряжен. эл. Поля	1 см-1	c2/G1/2	3.48 1024 эл.ст.ед 1.044 1029 в/м

Например, требуется заряд электрона выразить в сантиметрах. В электростатической системе единиц его величина равна 4,8 ∙10^-10 [г^1/2см^3/2сек^-1], чтобы получить величину, измеряемую в сантиметрах,  это значение следует умножить на корень квадратный из гравитационной постоянной и разделить на квадрат скорости света. В результате получим e=1.38·10^-34 см. Эту чрезвычайно малую величину можно рассматривать как электрический радиус электрона. Но существенно меньшее расстояние представляет масса электрона, значение которой в сантиметрах получается умножением значения массы в граммах на значение гравитационной постоянной и делением на квадрат скорости света. В результате получится m_e=6.757·10^-56 см. Масса протона соответственно будет m_p=1.24·10^-52 см.

Как видно из таблицы масса, равная 1 см, является очень большой величиной. Поэтому систему единиц ЭГ  удобно использовать в астрофизике. Пример подобного использования можно найти в работе [4].