Следовательно, с точки зрения теории массового обслуживания поточную линию можно рассматривать как многофазную систему массового обслуживания, в которой каждая следующая по технологическому процессу фаза (позиция) может приступать к обслуживанию, если заявка уже обслужена на предыдущей фазе. Заявка считается полностью обслуженной в момент окончания обслуживания на последней фазе.
Важным является то обстоятельство, что входящий поток требований, поступающих на обслуживание в ремонтные цехи и поточные линии вагоноремонтного предприятия, отвечает условию простейшего потока, то есть обладает свойствами стационарности ординарности и отсутствия последствий.
Система массового обслуживания как математическая модель поточной линии имеет такие составные элементы (параметры): входящий поток объектов труда, очередь объектов труда, обслуживающую систему – каналы обслуживания (позиции и оборудование поточной линии) и выходящий поток готовых изделий (отремонтированные вагоны или отдельные части вагонов). Эта система характеризуется следующими параметрами: средним количеством изделий, поступающих на обслуживание nизд; интенсивностью поступления изделий на обслуживание (ремонт) l, то есть средним количеством изделий, поступающих в ремонт в
единицу времени (l = nизд / tпр); средним временем обслуживания – tоб и интенсивностью обслуживания m = 1 / tоб; средним количеством требований в очереди u; средним временем ожидания в очереди на обработку tож = u / l; средним числом находящихся в очереди изделий
k = m / m – l.
Отношение интенсивности поступления изделий в ремонт к интенсивности их обработки на поточной линии характеризует степень загруженности линии r. Так, при
r =l / m > 1 (здесь l > m) линия будет перегружена, так как интенсивность поступления изделий превосходит интенсивность их обслуживания.
В установившемся режиме работы интенсивность процесса поступления изделий l ниже номинальной интенсивности их обработки m и тогда r < 1. В этом случае вероятность простаивания линии из-за отсутствия изделий будет Po = 1 – r. Тогда вероятность того, что в зоне поточной линии находится n изделий, будет Pn = (1 – r) rn.
|
|
|
Аналитическая теория массового обслуживания дает расчетные формулы, позволяющие определить важные характеристики качества функционирования производственных систем вагоноремонтного предприятия.
Рассмотрим пример анализа системы массового обслуживания применительно к лоточной линии. Пусть на поточной линии обрабатываются (ремонтируются) изделия, которые поступают в цех в случайном порядке с определенной плотностью, характеризующейся средней частотой поступления изделий в единицу времени. Пусть также известны статистическое распределение и среднее значение времени, затрачиваемого на ремонт изделия. Количественный анализ системы может дать ответы на следующие вопросы: каков средний размер возникающей время от времени очереди; какова вероятность того, что поступившее в ремонт изделие должно ждать своей очереди, так как линия (участок) занята обработкой изделий, поступивших ранее; какова степень загруженности линии в смену и т. д.
Предположим, что на поточную линию поступают в среднем 12 изделий в 1 ч или l = 12/60 = 0,2 изделия в 1 мин, а обработка занимает 4 мин, то есть интенсивность обслуживания m = 1/4 = 0,25 изделия в 1 мин. Принимая, что величина интервалов между поступлениями изделий и время ремонта подчиняются показательному закону распределения, в результате расчета получим следующие ответы. Средний размер очереди будет равен k = 0,25/ 0,25–0,2 = 4 изделия. Вероятность того, что изделие должно ждать очереди, составит 0,2/ 0,25 = 0,8. Степень загруженности линии r = l / m = 0,2/ 0,25 = 0,8 продолжительности смены, то есть 80% времени система занята обслуживанием. В случае увеличения интенсивности поступления изделий в ремонт (при l > m) потребуется перестройка режимов работы линии.
Таким образом, полученные в ходе расчета величины являются характеристиками отдельных свойств исследуемой системы, которые используются для анализа работы поточной линии и перестройки ее в нужном направлении.
Для оценки работы поточных линий применяют коэффициенты использования рабочего времени отдельной позиции и поточной линии в целом.
Коэффициент использования рабочего времени позиции поточной линии с периодическим перемещением изделий определяется отношением затраты рабочего времени на ремонт или изготовление изделия на этой позиции к величине ритма
|
(55)
где Dt – потери рабочего времени из-за неравномерной трудоемкости и нечеткой согласованности операций на позициях линии, мин.
Если по технологическому процессу обеспечивается полное использование рабочего времени на позициях потока, то есть Dt = 0, тогда коэффициент использования времени на каждой позиции будет
|
Коэффициент использования рабочего времени на поточной линии с периодическим перемещением изделий определяется как произведение коэффициента hпоз для каждой позиции на количество позиций поточной линии qп и после необходимых преобразований определяется по формуле
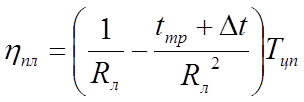 |
где Тцп – время действия (цикл) поточной линии Тцп = qп Rл.
Величины коэффициентов hпоз и hпл показывают, насколько производственный процесс рационально организовывая на каждой позиции потока и согласован с выбранной величиной ритма. Чем ближе значения этих коэффициентов к единице, тем удачнее выбраны основные параметры поточной линии. Пользуясь формулой (57), можно установить оптимальное значение ритма поточной линии при данных величинах потерь tтри Dt. На рис. 12 показаны кривые, характеризующие изменение hпл в зависимости от Rл при разных значениях tтр в условиях полной синхронизации позиций поточной линии, то есть при Dt =0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.