Методика построения эмпирической плотности распределения случайной величины и расчета ее характеристик. Определение вида закона распределения случайной величины и расчет его параметров при помощи метода моментов

1.Первичный анализ экспериментальных данных

1.1  Результаты 84 наблюдений в виде вариационного ряда в возрастающем порядке:

Таблица 1.1                                                                                                   

23,44	25,56	26,3	26,7	27,12	27,84	28,92
24,2	25,56	26,39	26,72	27,3	27,85	28,92
24,3	25,6	26,4	26,8	27,3	27,88	29,1
25,2	25,71	26,41	26,8	27,35	27,9	29,14
25,2	25,8	26,42	26,8	27,4	27,9	29,2
25,29	25,8	26,48	26,82	27,54	27,95	29,5
25,3	25,83	26,5	26,84	27,6	28,1	29,5
25,3	25,86	26,56	26,91	27,7	28,4	29,9
25,3	25,9	26,59	26,91	27,7	28,4	30,2
25,48	26,1	26,6	27,1	27,72	28,75	30,3
25,5	26,1	26,7	27,1	27,74	28,8	30,6
25,5	26,15	26,7	27,1	27,82	28,9	31,9

1.2  Определим величину среднего выборочного значения , которая равна сумме всех n отдельных результатов измерений x₁, x₂,… , x_n, деленных на количество измерений:

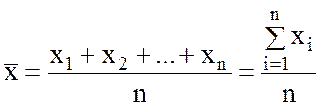; (1)

.

1.3  Корень квадратный из дисперсии, взятый с положительным знаком или выборочное среднеквадратическое отклонение:

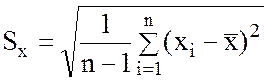; (2)

.

1.4  Проверка брака по условию:

; (3)

              где    x_n+1 – сомнительный результат измерений.

для значения 31,9:

;

 - браком не является (отбрасывать его нельзя).

Выполним проверку значения с помощью критерия Ирвина по формуле:

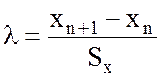; (4)

;

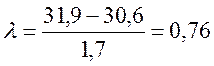По табл. 1.1 находим ближайшее n = 100, l_0,95=1,0. l_0,95=1,0>l=0,76. Поэтому значение 31,9 не является ошибкой, и мы его не отбрасываем.

2. Методика построения эмпирической плотности распределения

 случайной величины и расчета ее характеристик

2.1 Данные для расчета и построения плотности берем из первого задания.

Таблица 2.1

Исходные данные измеренных значений случайной величины

Результаты измерений										Xmax	Xmin
28,4	30,2	27,7	27,9	26,4	27,85	27,82	27,7	26,6	29,1	30,2	26,4
30,6	31,9	27,95	28,4	27,1	27,3	26,8	26,5	26,59	28,9	31,9	26,5
29,9	28,92	27,6	26,82	26,91	25,83	25,71	27,72	26,15	28,8	29,9	25,71
30,3	28,75	23,44	26,72	27,4	26,1	25,3	26,41	25,2	27,84	30,3	23,44
29,5	27,3	26,8	25,48	26,91	25,56	25,6	25,56	25,9	27,35	29,5	25,48
29,14	27,54	26,39	26,56	27,12	25,5	25,86	25,5	26,84	29,2	29,2	25,5
29,5	28,1	27,74	25,29	26,1	24,2	24,3	26,8	25,8	28,92	29,5	24,2
										31,9	23,44

По заданным результатам выборки необходимо вычислить выборочные значения: среднего, дисперсии и среднеквадратичного отклонения случайной величины. Построить гистограмму и эмпирическую функцию распределения вероятностей (кумулятивную кривую распределения).

Размах значений R:

                            R = х_max  - x_min = 31,9 – 23,44 =8,46; (т.к. n = 84, то принимаем количество интервалов k = 9).

         Тогда ширина интервала Δ:

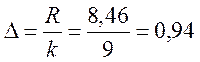. (5)

        Результаты подсчета частот и характеристик эмпирического распределения приведены в таблице 2.2.

 Таблица 2.2

Результаты подсчета частот и характеристик эмпирического распределения

Границы интервала группировки	Средин. значения интервала	Распределение данных	fi	u	uf	u^2*f
23,44…24,38	23,91	///	3	-3	-9	27
24,38…25,32	24,85	//////	6	-2	-12	24
25,32…26,26	25,79	///////////////	15	-1	-15	15
26,26…27,2	26,73	/////////////////////////	25	0	0	0
27,2…28,14	27,67	//////////////////	18	1	18	18
28,14…29,08	28,61	///////	7	2	14	28
29,08…30,02	29,55	//////	6	3	18	54
30,02…30,96	30,49	///	3	4	12	48
30,96…31,9	31,43	/	1	5	5	25
Итого			84	--	31	239

      Принимаем «ложный нуль» х₀ = 26,73 и обозначаем нулем (= 26,73) тот интервал, которому соответствует максимальная частота (f = 25).

      Выборочное среднее отклонение: 

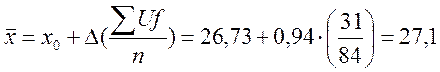  (6)

      Выборочное среднеквадратичное отклонение:

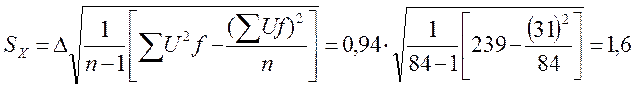 (7)

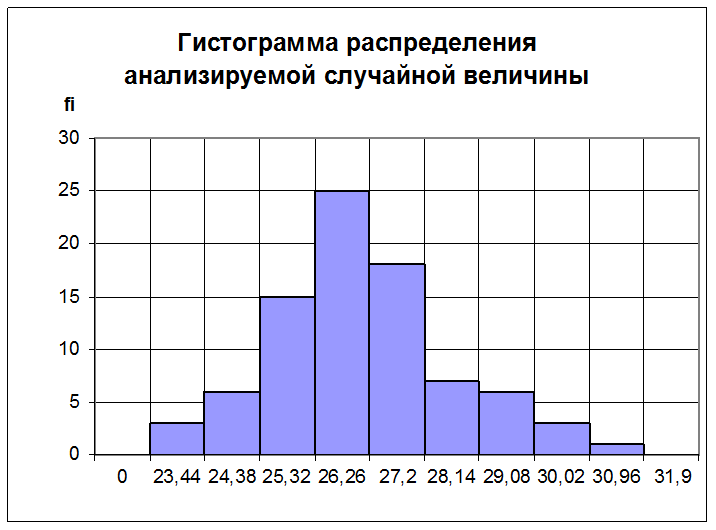
Рис.2.1.

Помимо гистограммы распределения случайной величины данные могут быть представлены также в виде кумулятивной кривой функции распределения вероятностей. Для этого данные, представленные в таблице 2.2, дополняем частостями (см. табл. 2.3).

Таблица 2.3

Таблица частот f и частостей ω

Границы интервала группировки	Частота, fi	Частость, ωi	Накопленная частость, ωн
23,44…24,38	3	0,036	0,036
24,38…25,32	6	0,071	0,107
25,32…26,26	15	0,179	0,286
26,26…27,2	25	0,298	0,584
27,2…28,14	18	0,214	0,798
28,14…29,08	7	0,083	0,881
29,08…30,02	6	0,071	0,952
30,02…30,96	3	0,036	0,988
30,96…31,9	1	0,012	1
Итого	84	1

        Кривая распределения накопленных частостей в виде ломаной линии, с числом звеньев, соответствующих количеству выбранных интервалов группировки анализируемых значений, представлена на рис. 2.2.

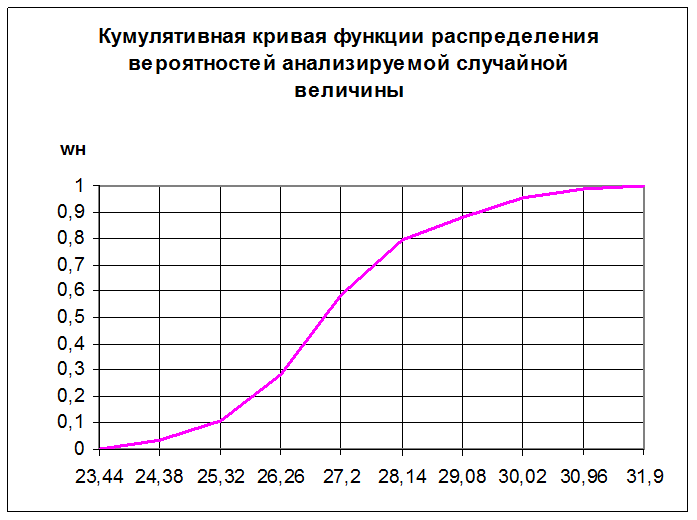
Рис. 2.2.