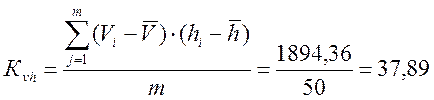 км/ч·
мм;
км/ч·
мм;
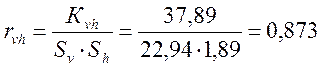 .
.
Мы установили, что между
анализируемыми величинами существует устойчивая статистическая связь. Теперь
необходимо установить аналитический вид этой связи. Для установления вида
аналитической связи между данными, представленными в табл. 5.1, выполним
следующие преобразования. Для каждого значения скорости движения тепловоза
рассчитываем значения средних величин перемещения верхней опорной плиты
роликовых опор кузова и строим график ![]() (см.
рис. 5.2).
(см.
рис. 5.2).
|
V |
|
|
40 |
2,98 |
|
60 |
4,17 |
|
80 |
5,93 |
|
100 |
7,3 |
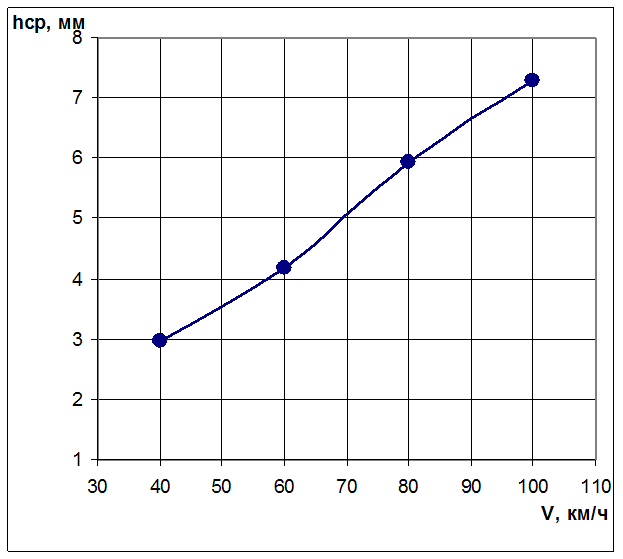
Рис. 5.2.
В нашем случае тенденция изменения парных значений, представленная на диаграмме рассеивания, приближается к линейной зависимости.
Так как известна величина коэффициента корреляции rxy , то определение параметров линейной регрессии выполняем, используя следующее соотношение:
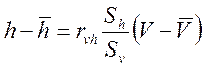 ; (23)
; (23)
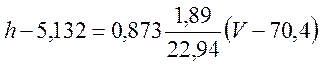 ;
;
![]() ;
;
![]() -
аналитический вид искомого уравнения.
-
аналитический вид искомого уравнения.
В качестве достоверности полученного уравнения регрессии используем величину среднеквадратической ошибки уравнения:
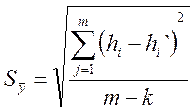 ; (24)
; (24)
где k – число параметров, используемых в подбираемом уравнении регрессии (k = 2).
Необходимые данные для расчета величины среднеквадратической ошибки уравнения представлены в табл. 5.3.
Таблица5.3
Данные для вычисления величины среднеквадратической ошибки
|
№ п/п |
|
|
|
|
|
1 |
40 |
2,943 |
2,98 |
0,001369 |
|
2 |
60 |
4,383 |
4,17 |
0,045369 |
|
3 |
80 |
5,823 |
5,93 |
0,011449 |
|
4 |
100 |
7,263 |
7,3 |
0,001369 |
|
Σ |
0,059556 |
Тогда:
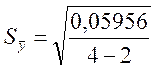 =
=![]() .
.
Так как выполняется условие ![]() (0,1726<0,5132),
то выравнивание линейной функцией признаем удовлетворительным. Это хорошо видно
на рис. 5.3.
(0,1726<0,5132),
то выравнивание линейной функцией признаем удовлетворительным. Это хорошо видно
на рис. 5.3.
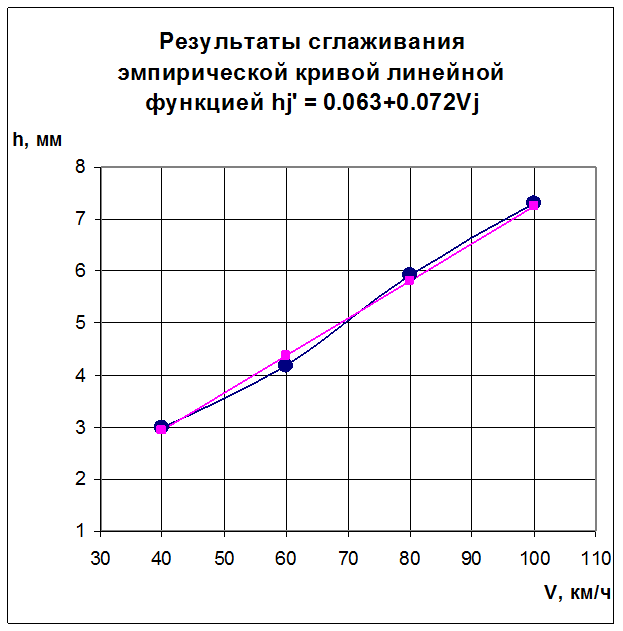
Рис. 5.3.
Величина среднеквадратической ошибки ![]() дает также
возможность определить доверительные границы для результативного признака.
дает также
возможность определить доверительные границы для результативного признака.
Величину доверительной вероятности принимаем ![]() .
.
Коэффициент Стьюдента, для принятой величины
доверительной вероятности и числа степеней свободы k = 50-2 = 48,
составляет ![]() (по табл. 1.1).
(по табл. 1.1).
Результаты расчета доверительных границ изменения перемещения опорной плиты роликовых опор кузова тепловоза 2ТЭ121 в зависимости от изменения скорости движения представлены в табл. 5.4.
Таблица 5.4
Результаты расчета доверительных границ
|
№ п/п |
|
|
|
|
|
|
|
1 |
35 |
2,583 |
0,8237 |
1,7593 |
3,4067 |
|
|
2 |
40 |
2,943 |
0,7437 |
2,1993 |
3,6867 |
|
|
3 |
45 |
3,303 |
0,6684 |
2,6346 |
3,9714 |
|
|
4 |
50 |
3,663 |
0,5995 |
3,0635 |
4,2625 |
|
|
5 |
55 |
4,023 |
0,5396 |
3,4834 |
4,5626 |
|
|
6 |
60 |
4,383 |
0,4919 |
3,8911 |
4,8749 |
|
|
7 |
65 |
4,743 |
0,4602 |
4,2828 |
5,2032 |
|
|
8 |
70 |
5,103 |
0,4480 |
4,6550 |
5,5510 |
|
|
9 |
75 |
5,463 |
0,4569 |
5,0061 |
5,9199 |
|
|
10 |
80 |
5,823 |
0,4856 |
5,3374 |
6,3086 |
|
|
11 |
85 |
6,183 |
0,5310 |
5,6520 |
6,7140 |
|
|
12 |
90 |
6,543 |
0,5892 |
5,9538 |
7,1322 |
|
|
13 |
95 |
6,903 |
0,6568 |
6,2462 |
7,5598 |
|
|
14 |
100 |
7,263 |
0,7313 |
6,5317 |
7,9943 |
|
|
15 |
105 |
7,623 |
0,8107 |
6,8123 |
8,4337 |
Характер расположения доверительных границ для
линейной регрессии ![]() представлен
на рис. 5.4.
представлен
на рис. 5.4.
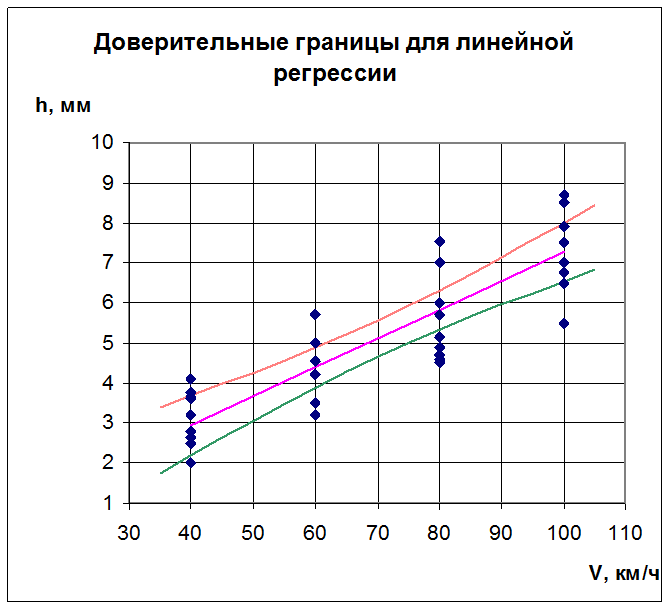
Рис. 5.4.
6. Оценка безотказности и прогнозирование ресурса элементов конструкций локомотивов
6.1. Расчет деталей на прочность с заданием уровня надежности
6.1.1. Вычисление вероятности безотказной работы элемента, когда его прочность и действующие нагрузки описываются нормальным законом распределения
Если прочность и напряжения описываются нормальными законами распределения, то случайная величина y также распределена по нормальному закону, а выражение для вероятности безотказной работы R имеет вид:
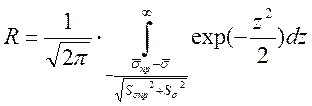 ;
(25)
;
(25)
где z – нормированная случайная величина, распределенная по нормальному
закону;
![]() - средние значения прочности и
напряжения;
- средние значения прочности и
напряжения;
![]() - средние квадратические отклонения
прочности и напряжения.
- средние квадратические отклонения
прочности и напряжения.
Поскольку ![]() нормированная случайная величина,
распределенная по нормальному закону, то вероятность безотказной работы
проектируемого элемента можно рассчитать с использованием табл.П.1.5[1] функции
нормального распределения в соответствии с выражением:
нормированная случайная величина,
распределенная по нормальному закону, то вероятность безотказной работы
проектируемого элемента можно рассчитать с использованием табл.П.1.5[1] функции
нормального распределения в соответствии с выражением:
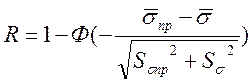 (26)
(26)
Используя выражение (26):
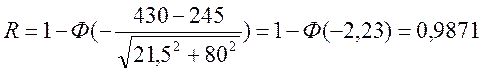 ;
;
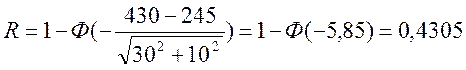 .
.
С помощью табл.П.1.5[1] для функции нормального распределения находим, что значение z, соответствующее вероятности безотказной работы R = 0,99, составляет -2,33. Подставляя это значение в нижний предел интегрирования выражения (25), получаем:
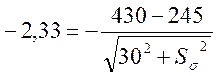 ;
;
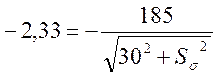 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() МПа.
МПа.
Результаты расчета вероятностей безотказной работы проектируемого элемента и среднего квадратического отклонения прочности представлены в табл.6.1.1.
Таблица 6.1.1
Вычисление вероятности безотказной работы элемента, когда его прочность и действующие нагрузки описываются нормальным законом распределения
|
|
|
|
|
|
R |
|
245 |
80 |
430 |
21,5 |
-2,23 |
0,98713 |
|
245 |
10 |
430 |
30 |
-5,85 |
0,43047 |
|
245 |
73,5 |
430 |
30 |
-2,33 |
0,99 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.