|
№ п/п |
|
|
|
|
|
|
|
|
|
1 |
40 |
-30,40 |
924,16 |
2 |
-3,132 |
9,809 |
95,213 |
|
|
2 |
40 |
-30,40 |
924,16 |
2 |
-3,132 |
9,809 |
95,213 |
|
|
3 |
40 |
-30,40 |
924,16 |
2,5 |
-2,632 |
6,927 |
80,013 |
|
|
4 |
40 |
-30,40 |
924,16 |
2,5 |
-2,632 |
6,927 |
80,013 |
|
|
5 |
40 |
-30,40 |
924,16 |
2,65 |
-2,482 |
6,160 |
75,453 |
|
|
6 |
40 |
-30,40 |
924,16 |
2,8 |
-2,332 |
5,438 |
70,893 |
|
|
7 |
40 |
-30,40 |
924,16 |
2,8 |
-2,332 |
5,438 |
70,893 |
|
|
8 |
40 |
-30,40 |
924,16 |
3,2 |
-1,932 |
3,733 |
58,733 |
|
|
9 |
40 |
-30,40 |
924,16 |
3,2 |
-1,932 |
3,733 |
58,733 |
|
|
10 |
40 |
-30,40 |
924,16 |
3,6 |
-1,532 |
2,347 |
46,573 |
|
|
11 |
40 |
-30,40 |
924,16 |
3,65 |
-1,482 |
2,196 |
45,053 |
|
|
12 |
40 |
-30,40 |
924,16 |
3,75 |
-1,382 |
1,910 |
42,013 |
|
|
13 |
40 |
-30,40 |
924,16 |
4,1 |
-1,032 |
1,065 |
31,373 |
|
|
14 |
60 |
-10,40 |
108,16 |
3,2 |
-1,932 |
3,733 |
20,093 |
|
|
15 |
60 |
-10,40 |
108,16 |
3,5 |
-1,632 |
2,663 |
16,973 |
|
|
16 |
60 |
-10,40 |
108,16 |
3,5 |
-1,632 |
2,663 |
16,973 |
|
|
17 |
60 |
-10,40 |
108,16 |
3,5 |
-1,632 |
2,663 |
16,973 |
|
|
18 |
60 |
-10,40 |
108,16 |
3,5 |
-1,632 |
2,663 |
16,973 |
|
|
19 |
60 |
-10,40 |
108,16 |
4,2 |
-0,932 |
0,869 |
9,693 |
|
|
20 |
60 |
-10,40 |
108,16 |
4,2 |
-0,932 |
0,869 |
9,693 |
|
|
21 |
60 |
-10,40 |
108,16 |
4,55 |
-0,582 |
0,339 |
6,053 |
|
|
22 |
60 |
-10,40 |
108,16 |
5 |
-0,132 |
0,017 |
1,373 |
|
|
23 |
60 |
-10,40 |
108,16 |
5 |
-0,132 |
0,017 |
1,373 |
|
|
24 |
60 |
-10,40 |
108,16 |
5,7 |
0,568 |
0,323 |
-5,907 |
|
|
25 |
80 |
9,60 |
92,16 |
4,5 |
-0,632 |
0,399 |
-6,067 |
|
|
26 |
80 |
9,60 |
92,16 |
4,6 |
-0,532 |
0,283 |
-5,107 |
|
|
27 |
80 |
9,60 |
92,16 |
4,7 |
-0,432 |
0,187 |
-4,147 |
|
|
28 |
80 |
9,60 |
92,16 |
4,9 |
-0,232 |
0,054 |
-2,227 |
|
|
29 |
80 |
9,60 |
92,16 |
5,15 |
0,018 |
0,000 |
0,173 |
|
|
30 |
80 |
9,60 |
92,16 |
5,7 |
0,568 |
0,323 |
5,453 |
|
|
31 |
80 |
9,60 |
92,16 |
6 |
0,868 |
0,753 |
8,333 |
|
|
32 |
80 |
9,60 |
92,16 |
6 |
0,868 |
0,753 |
8,333 |
|
|
33 |
80 |
9,60 |
92,16 |
7 |
1,868 |
3,489 |
17,933 |
|
|
34 |
80 |
9,60 |
92,16 |
7 |
1,868 |
3,489 |
17,933 |
|
|
35 |
80 |
9,60 |
92,16 |
7 |
1,868 |
3,489 |
17,933 |
|
|
36 |
80 |
9,60 |
92,16 |
7 |
1,868 |
3,489 |
17,933 |
|
|
37 |
80 |
9,60 |
92,16 |
7,55 |
2,418 |
5,847 |
23,213 |
|
|
38 |
100 |
29,60 |
876,16 |
6,5 |
1,368 |
1,871 |
40,493 |
|
|
39 |
100 |
29,60 |
876,16 |
5,5 |
0,368 |
0,135 |
10,893 |
|
|
40 |
100 |
29,60 |
876,16 |
6,75 |
1,618 |
2,618 |
47,893 |
|
|
41 |
100 |
29,60 |
876,16 |
6,75 |
1,618 |
2,618 |
47,893 |
|
|
42 |
100 |
29,60 |
876,16 |
7 |
1,868 |
3,489 |
55,293 |
|
|
43 |
100 |
29,60 |
876,16 |
7 |
1,868 |
3,489 |
55,293 |
|
|
44 |
100 |
29,60 |
876,16 |
7 |
1,868 |
3,489 |
55,293 |
|
|
45 |
100 |
29,60 |
876,16 |
7,5 |
2,368 |
5,607 |
70,093 |
|
|
46 |
100 |
29,60 |
876,16 |
7,9 |
2,768 |
7,662 |
81,933 |
|
|
47 |
100 |
29,60 |
876,16 |
7,9 |
2,768 |
7,662 |
81,933 |
|
|
48 |
100 |
29,60 |
876,16 |
7,9 |
2,768 |
7,662 |
81,933 |
|
|
49 |
100 |
29,60 |
876,16 |
8,5 |
3,368 |
11,343 |
99,693 |
|
|
50 |
100 |
29,60 |
876,16 |
8,7 |
3,568 |
12,731 |
105,613 |
|
|
Σ |
3520 |
0,00 |
25792,00 |
256,6 |
-0,868 |
175,249 |
1894,360 |
Используя результаты, представленные в табл. 5.2, находим соответствующие значения средних и среднеквадратических отклонений анализируемых величин:
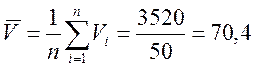 км/ч; (19)
км/ч; (19)
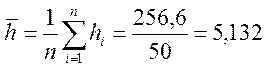 мм; (20)
мм; (20)
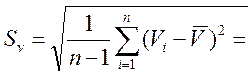
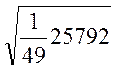 =
=![]() км/ч; (21)
км/ч; (21)
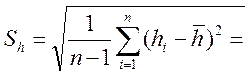
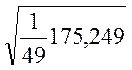 =
=![]() мм. (22)
мм. (22)
Используя (17) и (18), рассчитываем соответствующие значения коэффициентов ковариации и корреляции:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.