Другие предметы \ Основы теории надежности и диагностика

Методика построения эмпирической плотности распределения случайной величины и расчета ее характеристик. Определение вида закона распределения случайной величины и расчет его параметров при помощи метода моментов, страница 3

     Составляем таблицу 4.1, в которой рассчитываем накопленные по интервалам вероятности.

Таблица 4.1

Расчет координат эмпирических точек заданной выборки

№ п/п

li

fi, шт

Σfi

1

23,91

3

3

0,035

2

24,85

6

9

0,106

3

25,79

15

24

0,282

4

26,73

25

49

0,576

5

27,67

18

67

0,788

6

28,61

7

74

0,871

7

29,55

6

80

0,941

8

30,49

3

83

0,976

9

31,43

1

84

0,988

Двухпараметрическая плотность нормального закона распределения с параметром положения  и параметр формы  имеет вид:

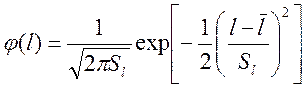. (12)

С помощью замены переменной 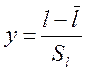 получаем выражение для нормированной функции нормального закона распределения:

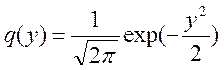.(13)

Масштаб значений оси абсцисс устанавливается на основе выражения:

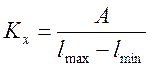; (14)

.

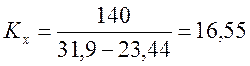Используя полученные в табл. 4.1 данные, строим вероятностную сетку на миллиметровой бумаге. Принимаем ширину графика А = 140 мм, высоту графика Н = 180 мм. Все необходимые значения для нанесения вероятностной сетки приведены в соответствии с выбранным масштабом в табл. 4.2.

Таблица 4.2

Координаты шкалы для построения вероятностной сетки нормального закона распределения

0,5

0,6

0,7

0,8

0,8413

0,85

0,903

0

0,25

0,52

0,85

1

1,05

1,3

0

7,5

15,6

25,5

30

31,5

39

0,96

0,971

0,98

0,991

0,9953

0,997

0,9987

1,75

1,9

2,05

2,35

2,6

2,75

3

52,5

57

61,5

70,5

78

82,5

90

На построенную вероятностную сетку наносим значения эмпирической функции распределения (см. столбец 5 табл. 4.1). Через отмеченные точки проводим прямую. Результаты построения представлены на рис. 4.1.

После построения необходимо произвести следующие расчеты:

                  Оценка среднего значения анализируемой случайной величины вычисляется на диаграмме при помощи ординаты ОВ:

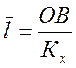;  (15)

                                                         

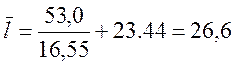
        Оценка среднеквадратического отклонения вычисляется на основе выражения:

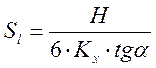; (16)

.

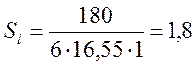5. Методика установления статистической

связи между случайными величинами

Таблица 5.1

Данные о перемещении опорной плиты роликовых опор кузова тепловоза 2ТЭ121 на прямых участках пути (h, мм) в зависимости от скорости движения тепловоза (V, км/ч)

V, км/ч

h, мм

40

2

2

2,5

2,5

2,65

2,8

2,8

3,2

3,2

3,6

3,65

3,75

4,1

60

3,2

3,5

3,5

3,5

3,5

4,2

4,2

4,55

5

5

5,7

80

4,5

4,6

4,7

4,9

5,15

5,7

6

6

7

7

7

7

7,55

100

6,5

5,5

6,75

6,75

7

7

7

7,5

7,9

7,9

7,9

8,5

8,7

Для установления количественной связи двух анализируемых случайных величин пользуются корреляционным моментом kxy и коэффициентом корреляции rxy. Корреляционный момент kxy двух непрерывных случайных величин X и Y вычисляется по формуле:

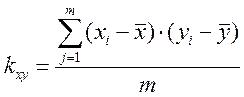; (17)

где   m – число пар анализируемых данных.

Тесноту корреляционной связи измеряют коэффициентом ковариации:

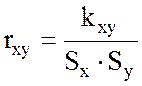.  (18)

В начале задания следует проанализировать исходные данные и построить диаграмму рассеивания. Используя табл. 5.1, наносим парные значения (V;h) и получаем диаграмму рассеивания, представленную на рис. 5.1.

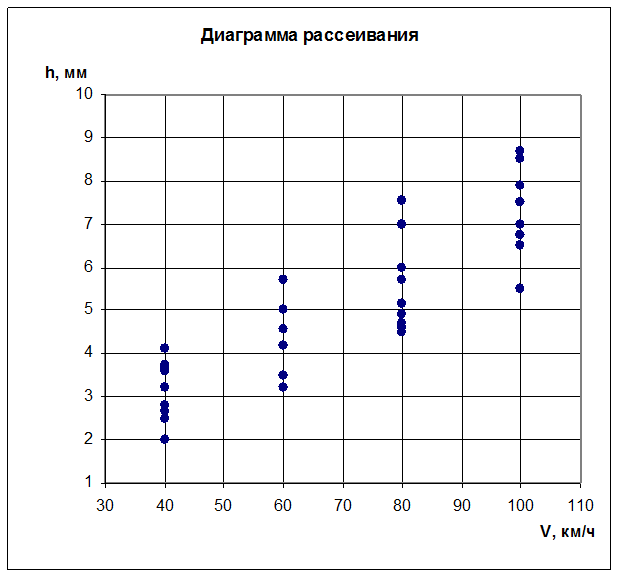
Рис. 5.1.

Теперь выполним необходимые преобразования исходных данных и представим их в табл. 5.2.

Таблица 5.2

Данные для расчета коэффициента корреляции между величиной перемещения верхней опорной плиты роликовых опор кузова тепловоза 2ТЭ121 в зависимости от скорости движения локомотива

Скачать файл