Методика построения эмпирической плотности распределения случайной величины и расчета ее характеристик. Определение вида закона распределения случайной величины и расчет его параметров при помощи метода моментов, страница 2

Из графика видим, что эмпирической вероятности 0,5 соответствует значение случайной величины . Т.е. аналитически рассчитанная величина эмпирического среднего  достаточно хорошо подтверждается и при графическом построении.

3. Определение вида закона распределения случайной величины

и расчет его параметров при помощи метода моментов

Требуется установить вид закона распределения данных, приведенных в п.1 и рассчитать параметры установленного закона распределения. Для этого надо провести обработку результатов и построить гистограмму распределения случайной величины (сделано в п.2).

Представленная на рис. 2.1 гистограмма имеет асимметрию, характерную для нормального (Гауссовского) закона распределения. Тогда проверку начнем именно с этого закона.

Плотность распределения вероятности нормального (Гауссовского) закона имеет вид:

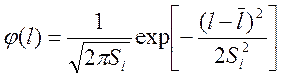, (8)

где    и  - параметры нормального закона распределения, величины которых мы рассчитали в п.1.

Для возможности использования в качестве справочных данных таблиц нормированного нормального распределения (табл. П1.4 приложения) в выражении (8) выполним замену переменных и их центрирование в соответствии с выражением:

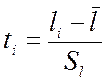,(9)

где    - середина i-того интервала группирования значений.

По найденным значениям  в табл. П1.4 находим значения  нормированного нормального распределения.

Затем рассчитываем значения теоретических вероятностей попадания в интервалы, используя выражение:

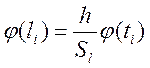,(10)

где    h – ширина интервала, рассчитанная в п. 2; h = 0,94.

Теоретические значения частот, выраженные через нормальный закон распределения:

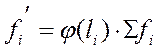 (11)

Все необходимые вычисления представлены в таблице 3.1.

Таблица 3.1

Последовательность аппроксимации эмпирического распределения нормальным (Гауссовским) законом

№ п/п	li	fi, шт	ti	φ(ti)	φ(li)	fi', шт
1	23,91	3	-2,035	0,0498	0,0301	2,53	0,0888
2	24,85	6	-1,431	0,1435	0,0867	7,28	0,2250
3	25,79	15	-0,827	0,2827	0,1707	14,34	0,0302
4	26,73	25	-0,223	0,3894	0,2352	19,75	1,3928
5	27,67	18	0,381	0,3712	0,2242	18,83	0,0367
6	28,61	7	0,985	0,2444	0,1476	12,40	2,3506
7	29,55	6	1,589	0,1127	0,0681	5,72	0,0140
8	30,49	3	2,193	0,03626	0,0219	1,84	0,7321
9	31,43	1	2,797	0,007915	0,0048	0,40	0,8920
Σ		84				83,09	5,7623

Нормальный закон распределения двухпараметрический. Поэтому число степеней свободы ν = k-c-1= 9-2-1= 6. Для величины ν = 6 и уровня значимости 0,05 по таблице П1.1приложения находим величину  = 12,592. Поскольку  рассчитанное в табл. 3.1 значение  = 5,7623 не превышает нормированную величину  =12,592, то эмпирическое распределение сглаживается нормальным законом, что подтверждается и графически (см. рис.3.1).

 Для наглядности проверим еще некоторые законы распределения, чтобы убедиться, что они не подходят для наших данных, и, следовательно, выбранный нами закон верный. Для краткости представим только таблицу и проверку.

Распределение Вейбулла-Гнеденко не подходит, т. к. величина выборочного коэффициента вариации равна:

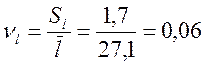; а для распределения Вейбулла-Гнеденко необходимо иметь ≈0,3

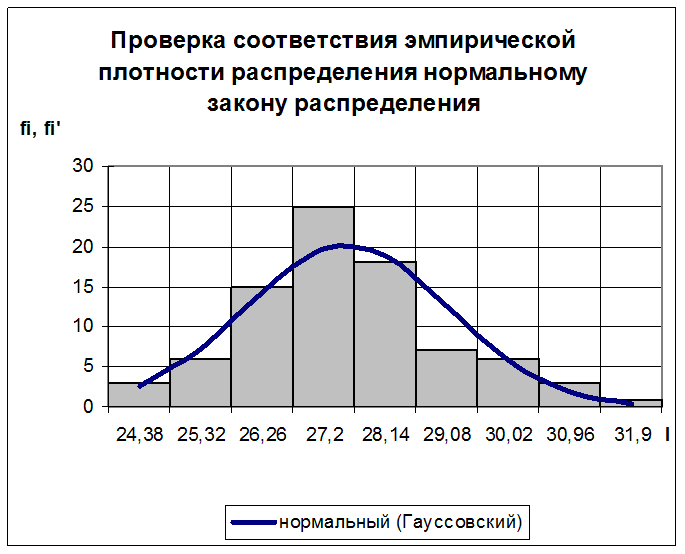
Рис. 3.1.

Таблица 3.2

Последовательность аппроксимации эмпирического распределения логарифмически-нормальным законом

№ п/п	li	fi, шт	lg¯l	S(lg l)	ti	φ(ti)	φ(li)	fi', шт
1	23,91	3	0,049	1,4312627	0,929	0,2589	0,049	3,870	0,196
2	24,85	6	0,100	1,428637	0,907	0,2637	0,046	3,663	1,491
3	25,79	15	0,252	1,4097555	0,822	0,285	0,042	3,309	41,296
4	26,73	25	0,425	1,3676861	0,733	0,3056	0,039	3,069	156,690
5	27,67	18	0,309	1,3983758	0,810	0,2874	0,039	3,084	72,151
6	28,61	7	0,121	1,4269565	0,936	0,2565	0,041	3,275	4,238
7	29,55	6	0,105	1,428252	0,956	0,2516	0,041	3,229	2,377
8	30,49	3	0,053	1,4311281	1,000	0,242	0,041	3,247	0,019
9	31,43	1	0,018	1,4319984	1,033	0,2347	0,041	3,246	1,554
Σ		84						29,994	280,012

 Логарифмически-нормальный закон  двухпараметрический, и, следовательно, как и ранее υ = 6,  = 12,592. Отсюда видно, что, полученное значение =280,012>12,592, что не допустимо. Следовательно, закон не подходит.

4. Определение вида теоретического закона распределения

случайной величины графическими методами

Общая методика оценки согласности закона распределения следующая:

-  подсчитывается накопленное количество значений случайной величины в каждом интервале группирования;

-  в соответствии с 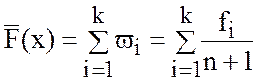 вычисляется оценка P=F(x);

-  на бумаге строится вероятностная сетка закона распределения случайной величины.