1.Первичный анализ экспериментальных данных
Количество НР тепловоза 2ТЭ10В в процессе эксплуатации: 0.686, 0.586, 0.522, 0.69, 0.525, 0.44, 0.234, 0.304, 0.297, 0.45, 0.475, 0.579, 0.536, 0.551, 0.467, 0.464, 0.5, 0.348, 0.31, 0.432, 0.51, 0.357, 0.43, 0.722, 0.433, 0.798, 0.483, 0.336, 0.341, 0.225, 0.389, 0.675, 0.771, 0.593, 0.868, 1.649, 1.146, 1.126, 1.083, 0.729, 0.545, 0.556, 0.606, 0.694, 0.47, 0.496, 0.968, 1.03, 1.05, 0.929, 0.919, 0.9, 0.842, 0.555, 0.601, 0.685, 0.54, 0.657, 0.503, 0.786, 1.526, 1.136, 1.225, 0.9, 0.641, 0.697, 1.146, 0.886, 0.755, 0.625, 0.489, 0.95, 1.33, 1.441, 2.045, 1.524, 1.126, 0.882, 1.691, 1.276, 1.023, 0.986, 1.051, 1.114
Количество НР тепловоза 2ТЭ10В в процессе эксплуатации в возрастающем порядке: 0.225, 0.234, 0.297, 0.304, 0.31, 0.336, 0.341, 0.348, 0.357, 0.389, 0.43, 0.432, 0.433, 0.44, 0.45, 0.464, 0.467, 0.47, 0.475, 0.483, 0.489, 0.496, 0.5, 0.503, 0.51, 0.522, 0.525, 0.536, 0.54, 0.545, 0.551, 0.555, 0.556, 0.579, 0.586, 0.593, 0.601, 0.606, 0.625, 0.641, 0.657, 0.675, 0.685, 0.686, 0.69, 0.694, 0.697, 0.722, 0.729, 0.755, 0.771, 0.786, 0.798, 0.842, 0.868, 0.882, 0.886, 0.9, 0.9, 0.919, 0.929, 0.95, 0.968, 0.986, 1.023, 1.03, 1.05, 1.051, 1.083, 1.141, 1.126, 1.126, 1.136, 1.146, 1.146, 1.225, 1.276, 1.33, 1.441, 1.524, 1.526, 1.649, 1.691, 2.045.
Величина выборочного среднего:
![]()
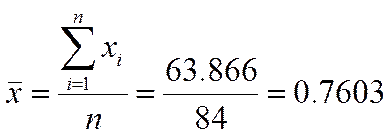
Среднеквадратическое отклонение или выборочный стандарт случайной величины:
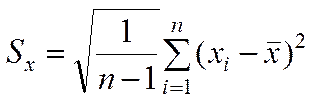
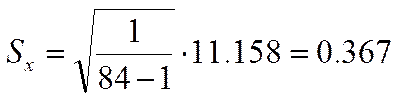
Берем необходимое условие брака:
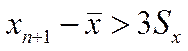
![]()
Отклонение от величины выборочной средней превышает предельную ошибку средней арифметической 3S, таким образом данное измерение является ошибочным и в дальнейших расчетах оно не применяется.
Величина выборочного среднего:
![]()
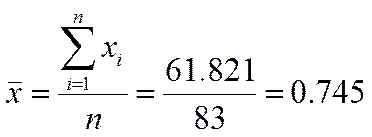
Среднеквадратическое отклонение или выборочный стандарт случайной величины:
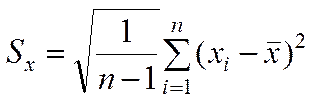
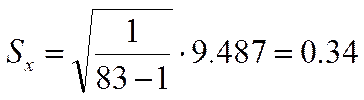
Берем необходимое условие брака:
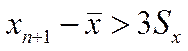
![]()
Отклонение от величины выборочной средней не превышает предельной ошибки средней арифметической 3S.
Выполняем подробную проверку с помощью критерия Ирвина:
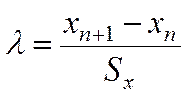
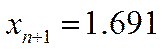
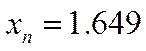
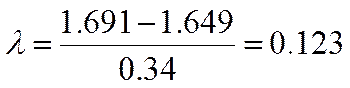
По таблице для ближайшего n=100, λ0.95=1
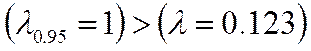
Поэтому значение 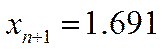 не является результатом
грубой ошибки и его отбрасывать нельзя
не является результатом
грубой ошибки и его отбрасывать нельзя
2. Построение эмпирической плотности распределения случайной величины и расчет ее характеристик
Размах:
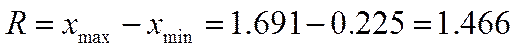
Таблица 2.1.
Результаты подсчета частот и характеристик эмпирического
распределения
|
Границы интервала группировки |
Средн. знач. интервалов |
Распределение данных |
fi |
u |
uf |
u2f |
|
|
0,225 |
0,388 |
0,306 |
///////// |
9 |
-1 |
-9 |
9 |
|
0,388 |
0,551 |
0,469 |
///////////////////////////// |
22 |
0 |
0 |
0 |
|
0,551 |
0,714 |
0,632 |
//////////////// |
16 |
1 |
16 |
16 |
|
0,714 |
0,877 |
0,795 |
//////// |
8 |
2 |
16 |
32 |
|
0,877 |
1,039 |
0,958 |
/////////// |
11 |
3 |
33 |
99 |
|
1,039 |
1,202 |
1,121 |
///////// |
9 |
4 |
36 |
144 |
|
1,202 |
1,365 |
1,284 |
/// |
3 |
5 |
15 |
75 |
|
1,365 |
1,528 |
1,447 |
/// |
3 |
6 |
18 |
108 |
|
1,528 |
1,691 |
1,610 |
// |
2 |
7 |
14 |
98 |
|
Итого |
83 |
139 |
581 |
||||
Ширина интервала:
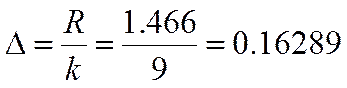
где k-количество интервалов (k=9)
Принимаем ложный нуль 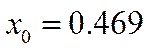 и обозначаем нулем тот
интервал, которому соответствует максимальная частота (f=22)
и обозначаем нулем тот
интервал, которому соответствует максимальная частота (f=22)
Выборочное среднее
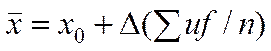
![]()
Среднеквадратическое отклонение:
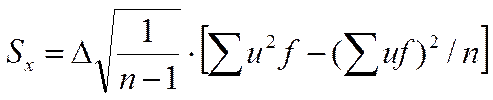
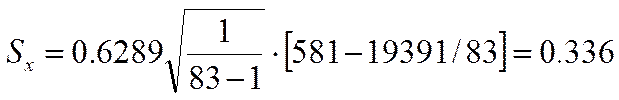
Таблица 2.2.
Таблица частот f и частостей w
|
Границы интервала группировки |
Частота, fi |
Частость, ωi |
Накопленная частость, ωн |
|
|
0,225 |
0,388 |
9 |
0,108433735 |
0,108433735 |
|
0,388 |
0,551 |
22 |
0,265060241 |
0,373493976 |
|
0,551 |
0,714 |
16 |
0,192771084 |
0,56626506 |
|
0,714 |
0,877 |
8 |
0,096385542 |
0,662650602 |
|
0,877 |
1,039 |
11 |
0,13253012 |
0,795180723 |
|
1,039 |
1,202 |
9 |
0,108433735 |
0,903614458 |
|
1,202 |
1,365 |
3 |
0,036144578 |
0,939759036 |
|
1,365 |
1,528 |
3 |
0,036144578 |
0,975903614 |
|
1,528 |
1,691 |
2 |
0,024096386 |
1 |
|
Итого |
83 |
1 |
||
Гистограмма распределения анализируемой случайной величины
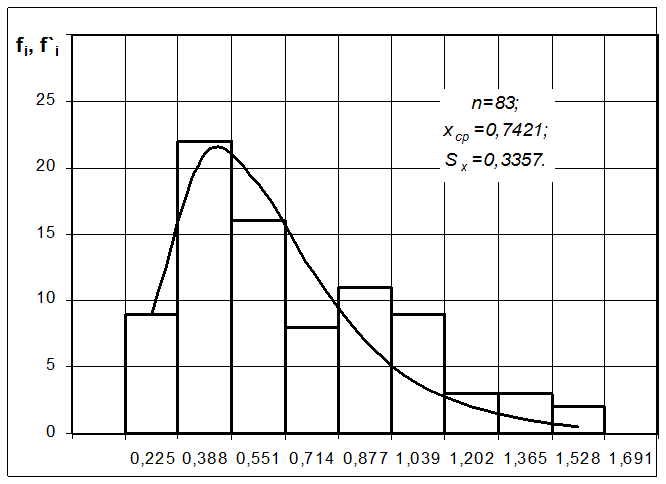
Рис. 2.1.
Эмпирическая кривая функции распределения вероятностей
анализируемой случайной величины
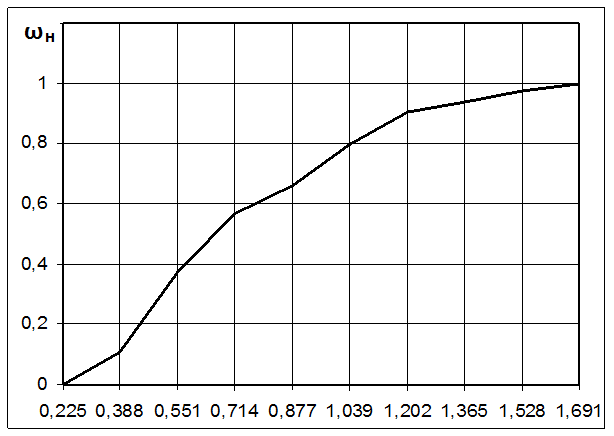
Рис. 2.2.
3. Определение вида закона распределения случайной величины и расчет его параметров при помощи метода моментов
Представленная на рис. 2.1. гистограмма имеет хорошо выраженную левостороннюю асимметрию, характерную для таких теоретических законов распределения, как логарифмически-нормальный и закон распределения Вейбулла-Гнеденко.
Логарифмически-нормальный закон
Таблица 3.1.
Плотность аппроксимации эмпирического распределения
логарифмически-нормальным законом
|
№ п/п |
li |
fi, шт |
ti |
φ(ti) |
φ(li) |
f'i |
(fi-f'i)^2/f'i |
|
1 |
0,306 |
9 |
-1,73466249 |
0,08933 |
0,645 |
8,71989 |
0,009 |
|
2 |
0,469 |
22 |
-0,79150985 |
0,292 |
1,377 |
18,6109 |
0,61717 |
|
3 |
0,632 |
16 |
-0,13233412 |
0,3956 |
1,384 |
18,7177 |
0,39459 |
|
4 |
0,795 |
8 |
0,37486963 |
0,3725 |
1,037 |
14,0141 |
2,5809 |
|
5 |
0,958 |
11 |
0,787210893 |
0,292 |
0,674 |
9,11765 |
0,38862 |
|
6 |
1,121 |
9 |
1,134644345 |
0,2107 |
0,416 |
5,62299 |
2,02814 |
|
7 |
1,284 |
3 |
1,434852493 |
0,1435 |
0,247 |
3,3437 |
0,03533 |
|
8 |
1,447 |
3 |
1,699150832 |
0,09405 |
0,144 |
1,94471 |
0,57264 |
|
9 |
1,610 |
2 |
1,935219624 |
0,06077 |
0,084 |
1,1294 |
0,6711 |
|
Σ |
83 |
81,221 |
7,29748 |
||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.