3. Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов
Требуется установить вид закона распределения величины количества отказов тепловоза 2ТЭ10В и рассчитать параметры установленного закона распределения.
Исходя из ранее полученной гистограммы распределения случайной величины, а также рекомендации преподавателя мною был выбран логарифмически-нормальный закон распределения, плотность вероятности которого имеет вид:
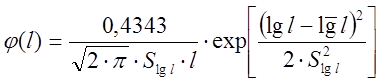 (7)
(7)
Процедура аппроксимации приведена в табл. 3. За случайную величину принимаем не li, а lgli. В связи с этим, новые значения выборочного среднего и среднеквадратического отклонения количества отказов тепловозов вычисляем по формулам:
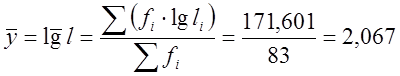 (8)
(8)
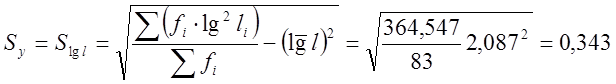 (9)
(9)
Производим центрирование эмпирических данных, используя выражение:
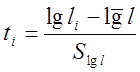 (10)
(10)
Соответствующие значения функции φ(ti) определяем с использованием функции плотности нормированного нормального распределения:
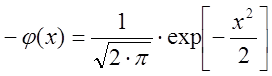 (11)
(11)
Значения теоретической вероятности φ(li) для соответствующих интервалов группирования вычисляем по формуле:
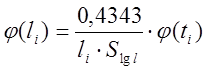 (12)
(12)
Теоретические значения частот ![]() ,
соответствующих логарифмически-нормальному закону распределения, находим в
соответствии с выражением:
,
соответствующих логарифмически-нормальному закону распределения, находим в
соответствии с выражением:
![]() (13)
(13)
Последовательность аппроксимации эмпирического распределения логарифмически-нормальным законом
Таблица 3.
|
№ п/п |
X i, ч |
f i, шт |
f i∙lgX i |
f i∙lg^2X i |
t i |
φ(t i) |
φ(X i)=0,4343∙φ(t i)/X i∙SlgX |
f ` i=φ(X i)∙h∙∑f i |
(f i - f ` i)^2/f ` i |
|
1 |
48,17 |
31 |
52,166 |
87,782 |
-1,122 |
0 |
0,000449 |
2,369 |
345,986 |
|
2 |
111,71 |
17 |
34,817 |
71,308 |
-0,057 |
0,1 |
0,000650 |
3,425 |
53,795 |
|
3 |
175,24 |
12 |
26,924 |
60,407 |
0,514 |
0,1 |
0,001037 |
5,468 |
7,802 |
|
4 |
238,78 |
7 |
16,646 |
39,584 |
0,905 |
0,3 |
0,001386 |
7,308 |
0,013 |
|
5 |
302,32 |
7 |
17,363 |
43,069 |
1,204 |
0,4 |
0,001530 |
8,069 |
0,142 |
|
6 |
365,85 |
5 |
12,817 |
32,853 |
1,446 |
0,4 |
0,001378 |
7,268 |
0,708 |
|
7 |
429,39 |
1 |
2,633 |
6,932 |
1,648 |
0,3 |
0,001022 |
5,392 |
3,577 |
|
8 |
492,93 |
0 |
0,000 |
0,000 |
1,823 |
0,2 |
0,000628 |
3,311 |
3,311 |
|
9 |
556,46 |
3 |
8,236 |
22,612 |
1,977 |
0,1 |
0,000322 |
1,698 |
0,998 |
|
∑ |
83 |
171,601 |
364,547 |
44,308 |
416,333 |
Логарифмически-нормальный закон распределения
двухпараметрический, и, следовательно, ![]() и
и
![]() . Поскольку в результате расчета
. Поскольку в результате расчета ![]() и
и ![]() ,
то эмпирическое распределение сглаживается логарифмически нормальным законом.
,
то эмпирическое распределение сглаживается логарифмически нормальным законом.
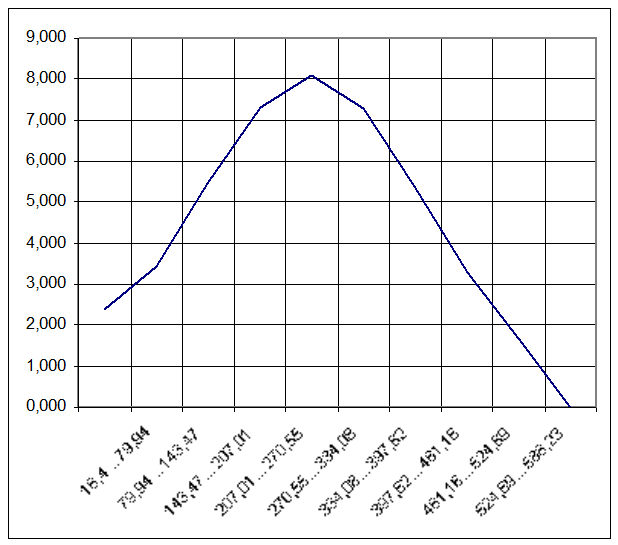
Рис. 3
Принимая полученные ранее оценки математического
ожидания ![]() и стандарта
и стандарта ![]() в
качестве параметров теоретического закона распределения, плотность
распределения количества отказов тепловоза 2ТЭ10В можно записать в виде:
в
качестве параметров теоретического закона распределения, плотность
распределения количества отказов тепловоза 2ТЭ10В можно записать в виде:
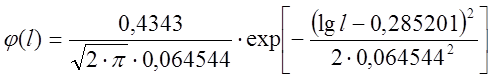
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.