Определение вида закона распределения случайной величины и расчет его параметров при помощи метода моментов. Расчет деталей на прочность с заданием уровня надежности, страница 2

Так как за случайную величину принимаем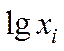

Выборочное среднее

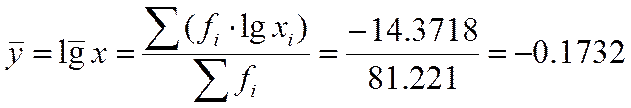
Среднеквадратическое отклонение наработок

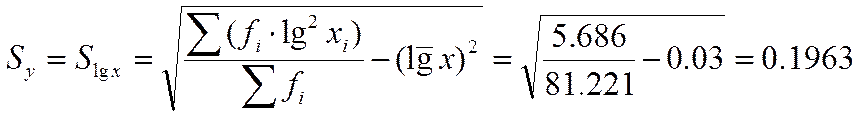
Центрирование эмпирических данных:

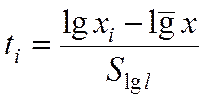
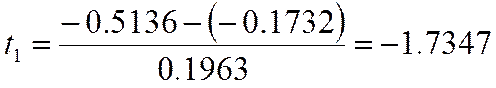
Соответствующие значения функции  φ(t) определяем с использованием функции плотности нормированного нормального распределения.

Значение теоретической вероятности  для соответствующих интервалов группирования:

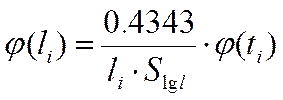
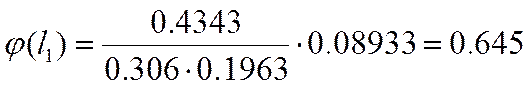
Теоретическое значение частот:

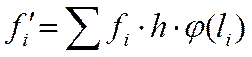
Наиболее подходящий закон распределения логарифмически-нормальный.

4. Определение вида теоретического закона распределения случайной величины графическими методами

Таблица 4.1.

Координаты шкалы для построения сетки логарифмически - нормального

закона распределения

P=F(x)	0,5	0,6	0,7	0,8	0,8413	0,85	0,903
y=Q-1(P)	0	0,25	0,52	0,85	1	1,05	1,3
Ky(P)	0	1,5	15,6	25,5	30	31,5	39
P=F(x)	0,96	0,971	0,98	0,991	0,9953	0,997	0,9987
y=Q-1(P)	1,75	1,9	2,05	2,35	2,6	2,75	3
Ky(P)	52,5	57	61,5	70,5	78	82,5	90

Таблица 4.2.

Расчет координат эмпирических точек заданной выборки

№ п/п	среднее значение интервала, li	Kx(li)=146,06*lgli	F(l)=Σfi/n+1
1	0,306	-75,02346304	0,10714286
2	0,469	-47,9834267	0,36904762
3	0,632	-29,0849633	0,55952381
4	0,795	-14,54351225	0,6547619
5	0,958	-2,721753744	0,78571429
6	1,121	7,239108116	0,89285714
7	1,284	15,84602804	0,92857143
8	1,447	23,42341943	0,96428571
9	1,610	30,19147419	0,98809524

Масштаб значений оси абсцисс

А-ширина графика (А=140 мм)

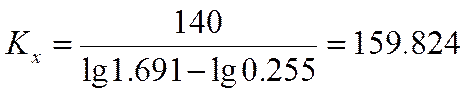
Текущие значения анализируемых случайных величин, которые наносятся на ось абсцисс

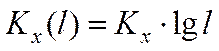
Минимальное значение наработки, с учетом полученного значения масштаба:

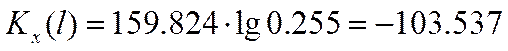
Максимальное значение

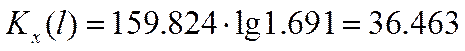
Отрезок ОВ позволяет определить оценку среднего значения случайной величины. Построенная на рис. 4.1. прямая дает нам возможность определить ОВ=-36.127 и tgα=0.892.

Оценка среднего значения случайной величины

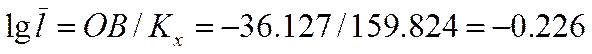
Оценка среднеквадратического отклонения случайной величины

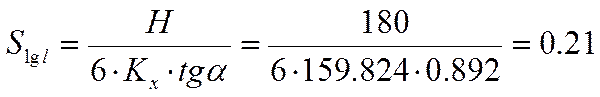
3. Расчет деталей на прочность с заданием уровня надежности

3.1. Вычислении вероятности безотказной работы элемента, когда его прочность и действующие нагрузки описываются нормальным законом распределения

Вероятность безотказной работы можно рассчитать с использованием функции нормального распределения в соответствии с выражением:

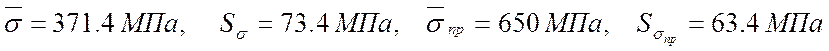
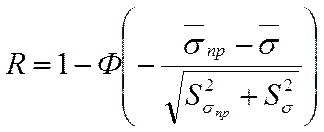
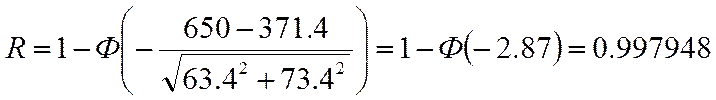
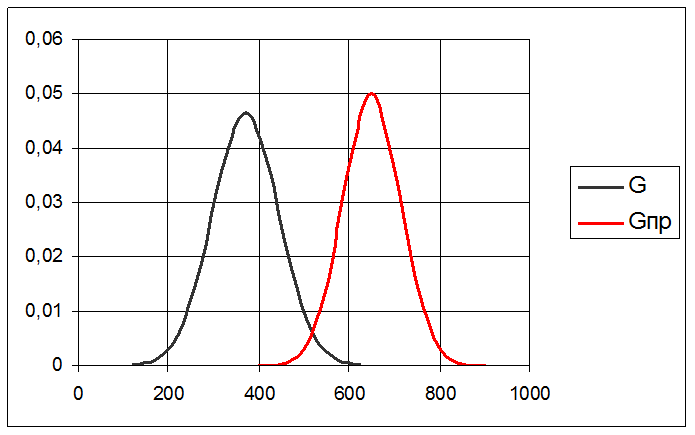
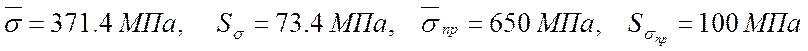
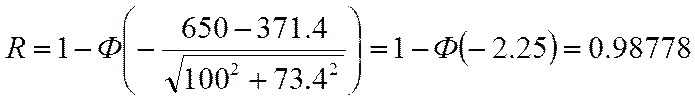
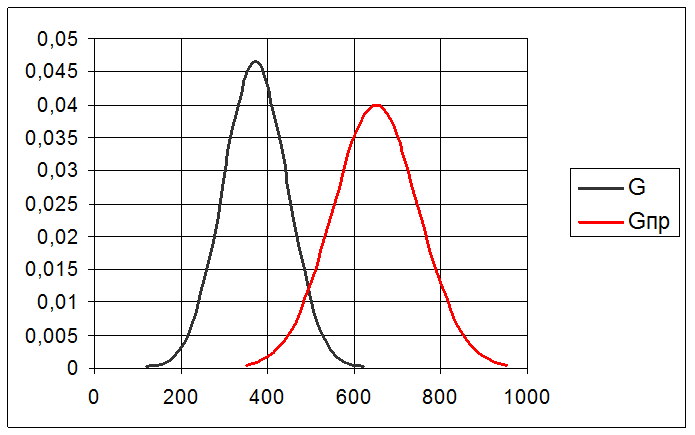
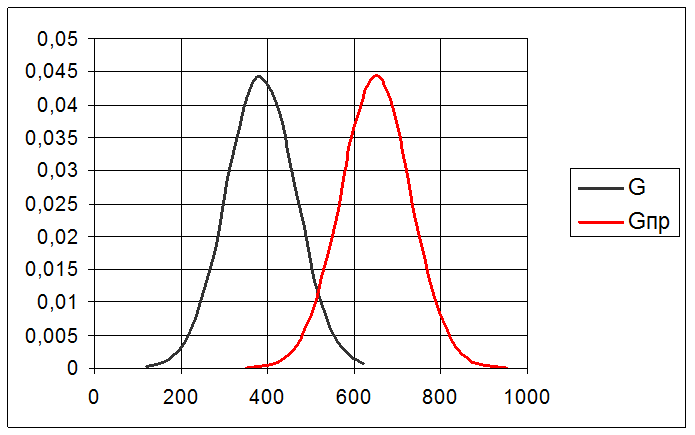
Максимальное значение среднего квадратического отклонения прочности, при котором гарантируется, что вероятность безотказной работы  элемента не окажется меньше 0.99

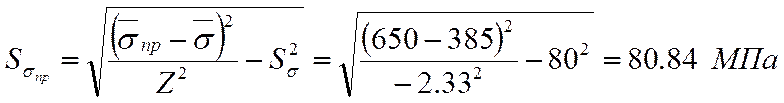
3.2. Вычисление вероятности безотказной работы элемента при нормальном распределении прочности и экспоненциальном распределении действующей нагрузки

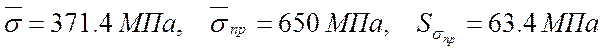
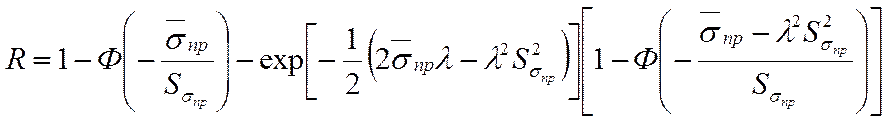
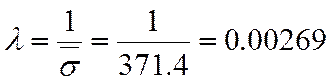
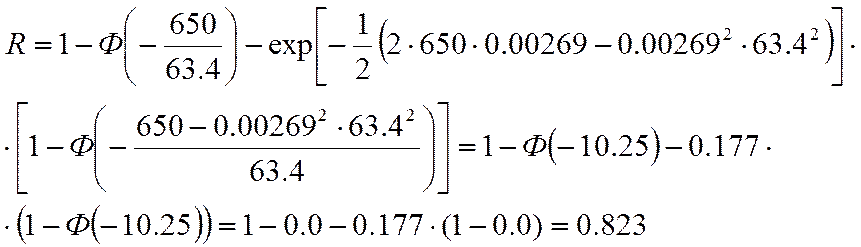
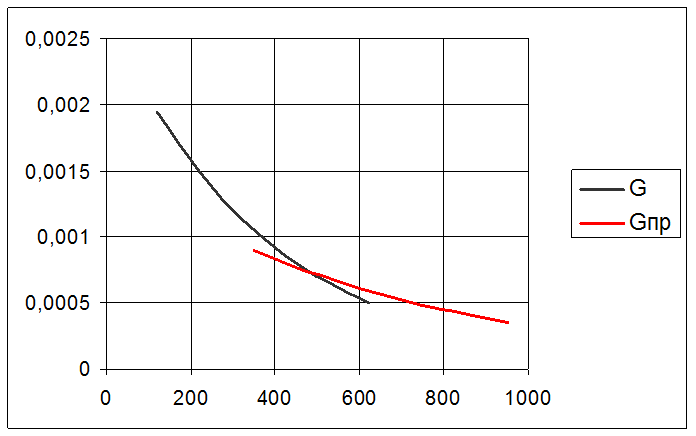
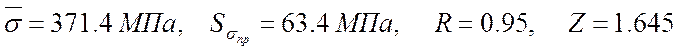
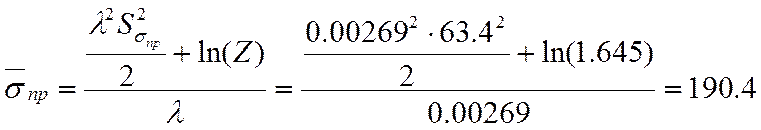
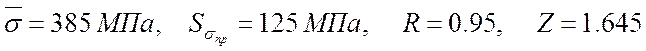
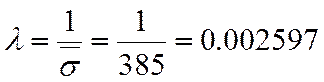
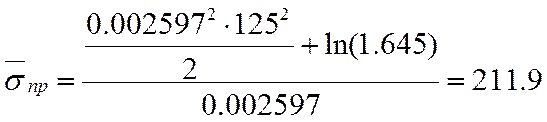
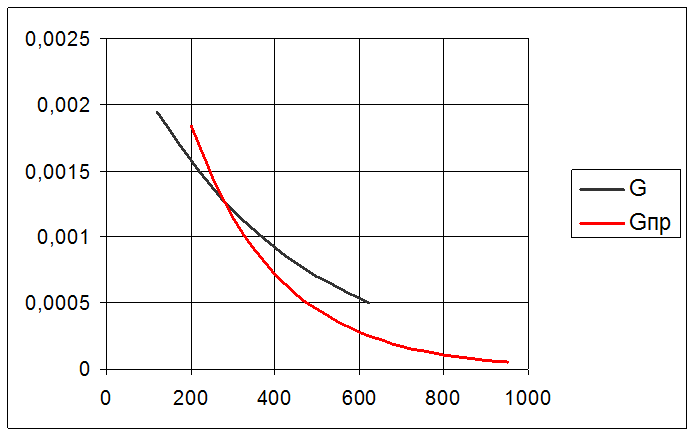
3.3. Вычисление вероятности безотказной работы элемента при нормальном законе распределения нагрузки и распределения прочности по закону Вейбула-Гнеденко

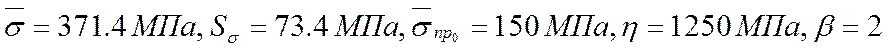
Находим параметра А и С

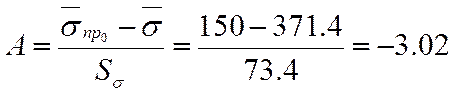
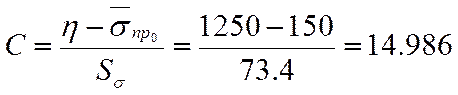
Используя данные приведенные в таблице определяем вероятность отказа элемента. Так, для  вероятность отказа .

Соответственно вероятность безотказной работы составит

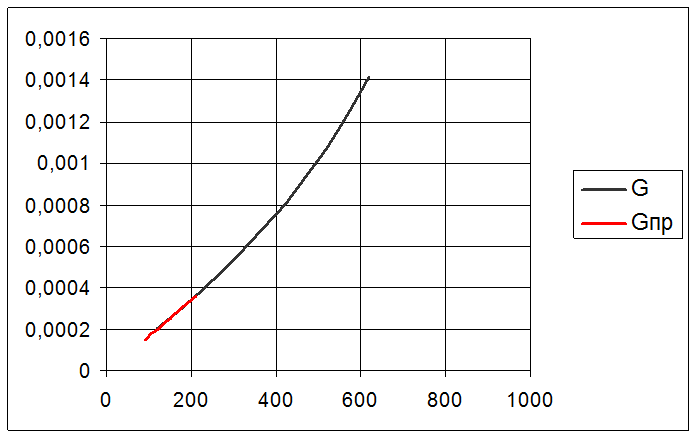
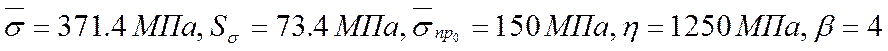
При  вероятность отказа .

Необходимо рассчитать требуемую характеристику прочности материала элемента конструкции, если известны:

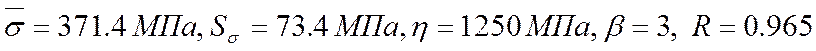
Находим параметра А и С

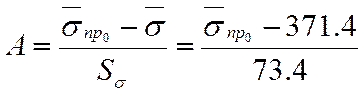
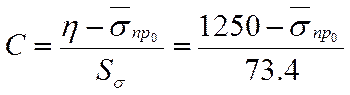
Исключая 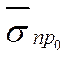, получаем

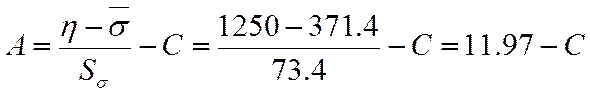
Из таблицы находим, что заданной вероятности отказа  соответствует величина . Тогда величина  и

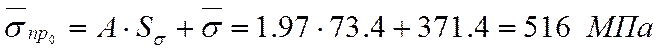
Необходимо определить параметры распределения действующей на элемент конструкции нагрузки.

Находим параметра А и С

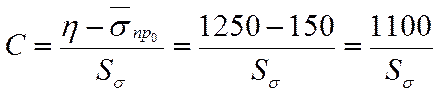
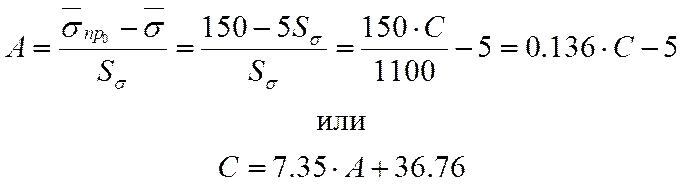
С помощью таблицы находим, что при  и  вероятность отказа составляет . Точное значение С при  будет равно , отсюда

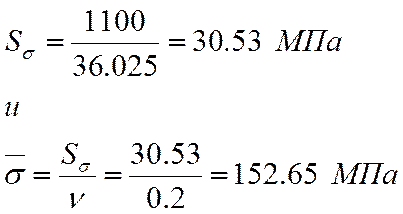
3.4. Оптимизация параметров прочности деталей в зависимости от уровня необходимых затрат

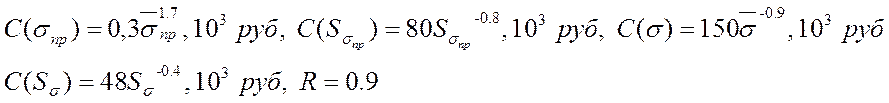
Используя уравнение связи, с помощью таблиц для нормированного нормального распределения находим величину . В этом случае задача минимизации состоит в следующем. Необходимо минимизировать общие затраты

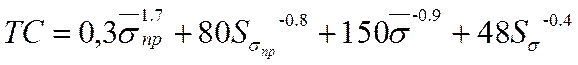
при ограничении

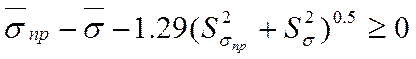
Получаем следующую систему уравнений:

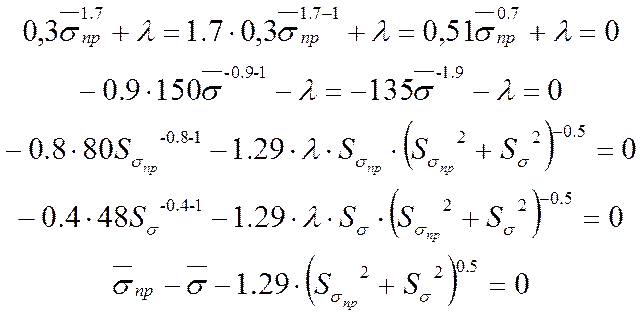
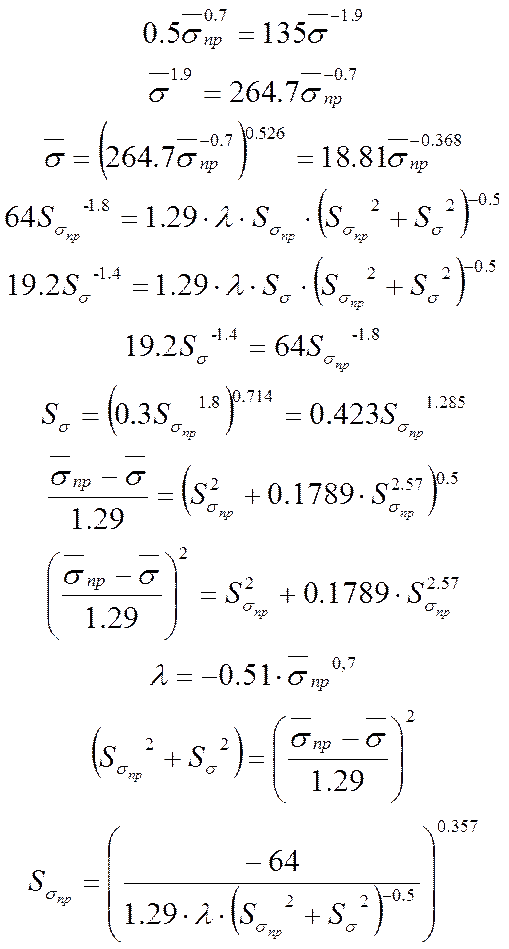
Задаемся предполагаемыми значениями  и заполняем таблицу 3.1.

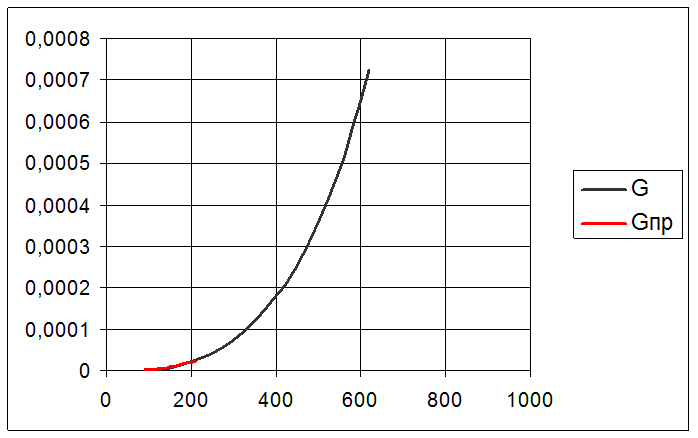
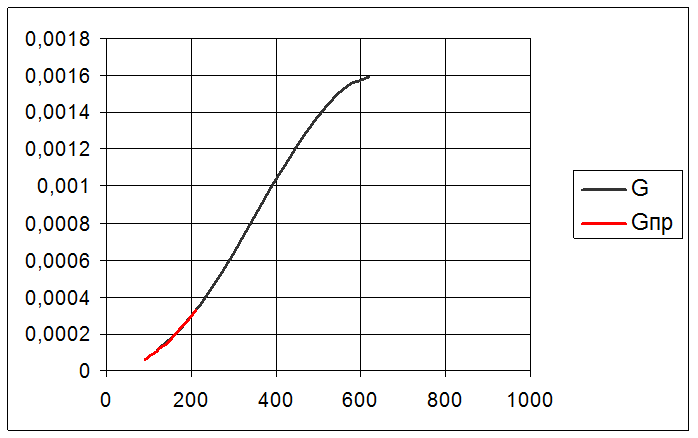
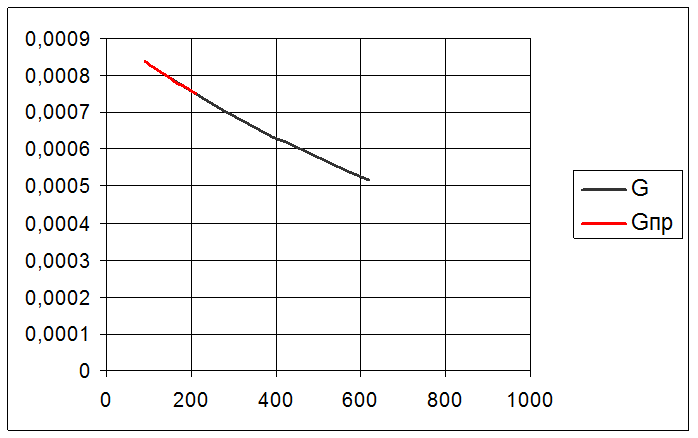
Кривая общих затрат как функция средней прочности

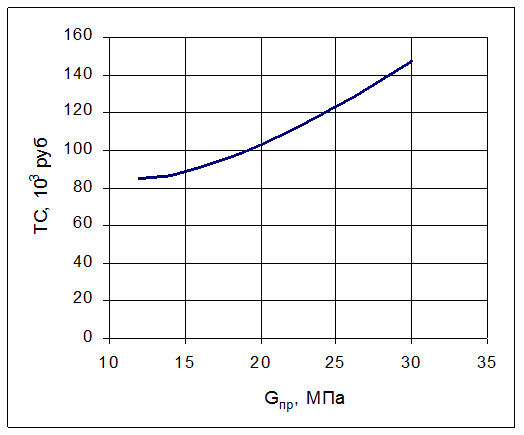
Рис. 3.1.

Из анализа графика  (рис. 3.1.)следует, что оптимальное значение . Соответствующие этому оптимуму значения 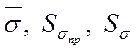 соответственно составляют: , , . Общие затраты на изготовление детали с требуемой вероятностью безотказной работы  составляют 85.026 тыс. руб.

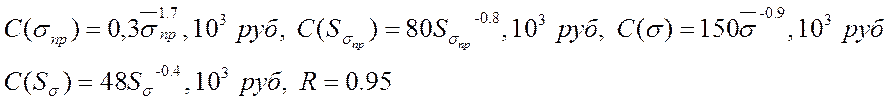
Используя уравнение связи, с помощью таблиц для нормированного нормального распределения находим величину .

Кривая общих затрат как функция средней прочности

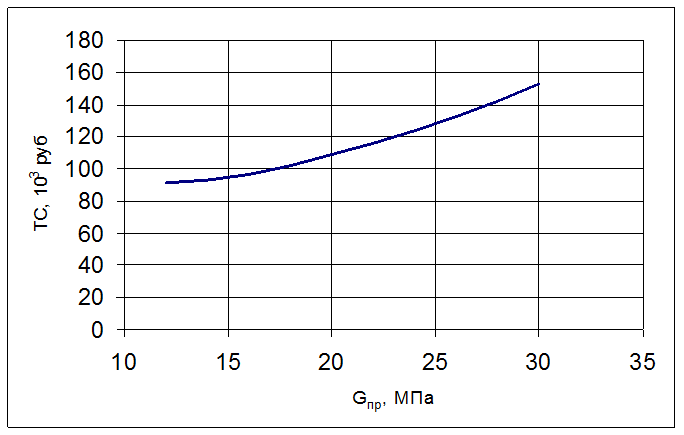
Рис. 3.2.

Из анализа графика  (рис. 3.2.)следует, что оптимальное значение . Соответствующие этому оптимуму значения 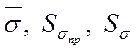 соответственно составляют: , , . Общие затраты на изготовление детали с требуемой вероятностью безотказной работы  составляют 91.644  тыс. руб.

Используя уравнение связи, с помощью таблиц для нормированного нормального распределения находим величину .

Кривая общих затрат как функция средней прочности

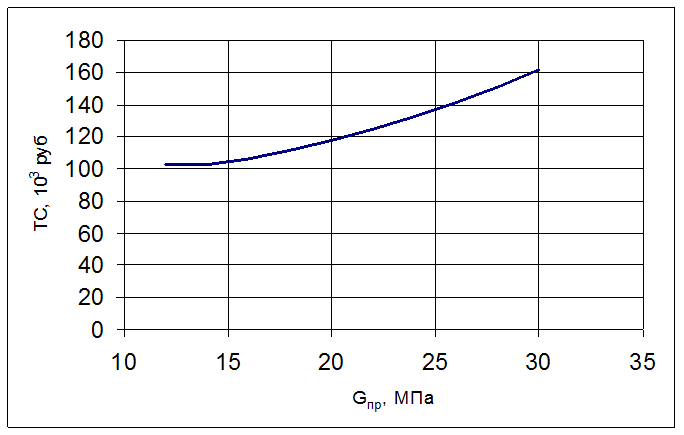
Рис. 3.3.

Из анализа графика  (рис. 3.3.)следует, что оптимальное значение . Соответствующие этому оптимуму значения 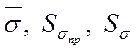 соответственно составляют: , , . Общие затраты на изготовление детали с требуемой вероятностью безотказной работы  составляют 102.813  тыс. руб.