3. Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов
Требуется установить вид закона распределения величины количества отказов тепловоза 2ТЭ10В и рассчитать параметры установленного закона распределения.
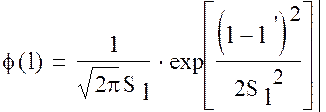 |
где, l` и Sl – параметры нормального закона распределения, велечины которых мы уже рассчитали ранее:
l`=3,277 Sl=0,2666
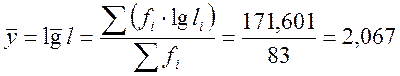
где, li – cередина i-го интервала группирования значений наработок дизелей на неплановый ремонт.
Все необходимые вычисления удобно выполнять в табл. 3. Прежде всего по найденным значениям ti в табл. П1.4 находим значения φ(ti) нормированного нормального распределения и заполняем (столбец 5).
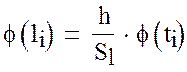 |
|||
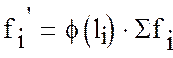 |
|||
Последовательность аппроксимации эмпирического распределения экспоненциальным законом
Таблица 3.
|
№ п/п |
X i, ч |
f i, шт |
λ∙X i |
exp(-λ∙X i) |
φ(X i)=λ∙exp(-λ∙X i) |
f ` i=φ(X i)∙h∙∑f i |
(f i - f ` i)^2/f ` i |
|
1 |
48,17 |
31 |
0,3036 |
0,738 |
0,0046526 |
24,54 |
1,703 |
|
2 |
111,71 |
17 |
0,7041 |
0,495 |
0,0031173 |
16,44 |
0,019 |
|
3 |
175,24 |
12 |
1,1046 |
0,331 |
0,0020886 |
11,01 |
0,088 |
|
4 |
238,78 |
7 |
1,5051 |
0,222 |
0,0013993 |
7,38 |
0,020 |
|
5 |
302,32 |
7 |
1,9055 |
0,149 |
0,0009376 |
4,94 |
0,855 |
|
6 |
365,85 |
5 |
2,3060 |
0,100 |
0,0006282 |
3,31 |
0,860 |
|
7 |
429,39 |
1 |
2,7065 |
0,067 |
0,0004209 |
2,22 |
0,670 |
|
8 |
492,93 |
0 |
3,1070 |
0,045 |
0,0002820 |
1,49 |
1,487 |
|
9 |
556,46 |
3 |
3,5075 |
0,030 |
0,0001889 |
1,00 |
4,030 |
|
∑ |
83 |
9,731 |
|
v=k-c-1 |
χ^2= |
9,731 |
|
|
v=9-1-1= |
7 |
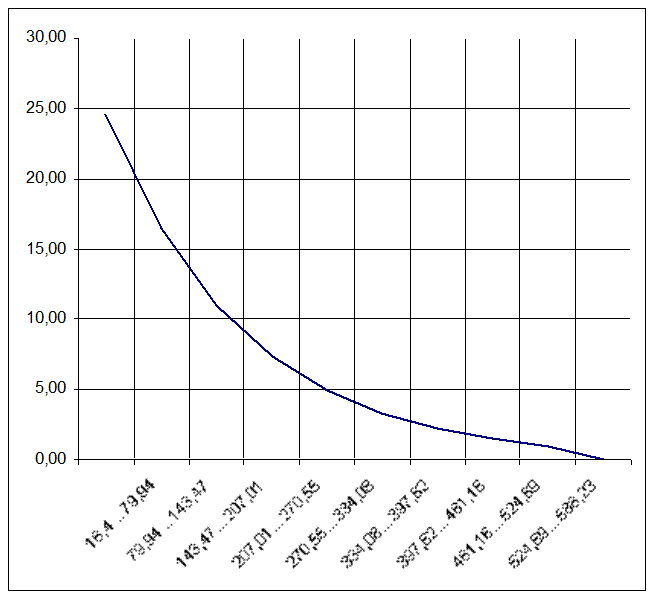
4. Определение вида теоретического закона распределения случайной величины графическими методами
Общая методика графической оценки согласованности закона распределения следующая:
- подсчитывается накопленное количество значений случайной величины в каждом интервале группирования;
- вычисляется оценка P = F(х) в соответствии c формулой:
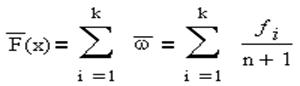
- на вероятностной бумаге, принятого к анализу закона распределения, наносятся точки с координатами:
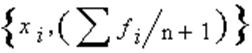
Если эти точки сравнительно хорошо ложатся на прямую линию, то принимается гипотеза о согласовании эмпирических данных рассматриваемому закону распределения. В противном случае, берётся вероятностная бумага, соответствующая другому закону распределения, и проверка повторяется.
Составляем табл.4., в которой рассчитываем накопленные по интервалам вероятности.
Расчёт координат эмпирических точек заданной выборки
Таблица 4.
|
№ п/п |
X i, ч |
f i, шт |
∑f i |
F(l)=∑f i/(n+1) |
|
1 |
48,17 |
31 |
31 |
0,369 |
|
2 |
111,71 |
17 |
48 |
0,571 |
|
3 |
175,24 |
12 |
60 |
0,714 |
|
4 |
238,78 |
7 |
67 |
0,798 |
|
5 |
302,32 |
7 |
74 |
0,881 |
|
6 |
365,85 |
5 |
79 |
0,940 |
|
7 |
429,39 |
1 |
80 |
0,952 |
|
8 |
492,93 |
0 |
80 |
0,952 |
|
9 |
556,46 |
3 |
83 |
0,988 |
Используя полученные в табл.4. данные, строим вероятностную сетку и выполняем проверку согласованности.
Выбор масштаба построения вероятностной сетки:
· ширина графика (ось абсцисс) А = 140 мм ;
· высота графика (ось ординат) Н = 180 мм .
Масштаб значений оси абсцисс устанавливается на основе выражения:
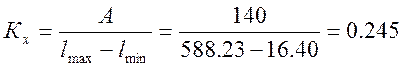
Оценка среднего значения анализируемой случайной величины вычисляется на диаграмме при помощи ординаты ОС
![]()
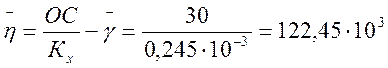
![]()
Уточняем значения оценок, т.к. горизонтальная ось начинается не из нуля, а от значения 16,40
![]()
![]()
![]()
![]()
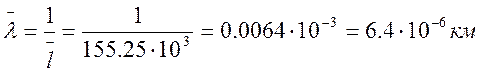
5. Методика установления статистической связи между случайными величинами
Данные для расчета коэффициента корреляции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.