Другие предметы \ Основы теории надежности и диагностика

Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов, страница 3

Используя результаты, представленные в табл. 5.1., находим соответствующие значения средних и среднеквадратичных отклонений анализируемых величин:

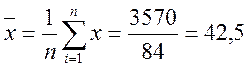
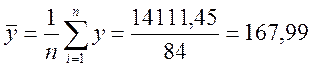
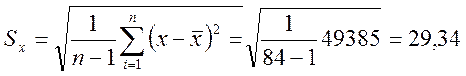
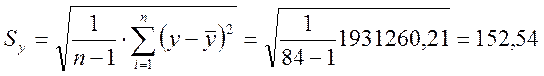
Рассчитываем соответствующие значения коэффициентов ковариации К_xtи корреляции r_xt

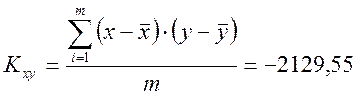
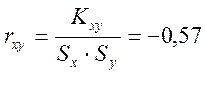
Начнём сглаживание с помощью наиболее подходящей линейной функции, уравнение которой имеет вид:

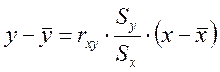
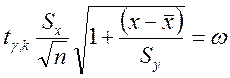
Проверка: 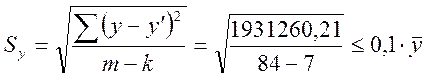; 162,65 < 0,1*167,99

Результаты расчёта доверительных границ

№ п/п	x	y	y	y'	y"
1	1	227,27	316,52538	261,90319	371,14757	54,62219
2	2	322,6	312,94629	259,299263	366,59333	53,64703
3	3	153,84	309,36721	256,688946	362,04548	52,67827
4	4	133,3	305,78813	254,071879	357,50438	51,71625
5	5	370,4	302,20905	251,447679	352,97042	50,76137
6	6	277,8	298,62996	248,815935	348,44399	49,81403
7	7	420,6	295,05088	246,176209	343,92556	48,87467
8	8	285,71	291,4718	243,528031	339,41557	47,94377
9	9	185,18	287,89272	240,8709	334,91453	47,02182
10	10	149,25	284,31363	238,204278	330,42299	46,10936
11	11	322,6	280,73455	235,527591	325,94151	45,20696
12	12	943,4	277,15547	232,840224	321,47072	44,31525
13	13	172,4	273,57639	230,141519	317,01126	43,43487
14	14	172,4	269,9973	227,430772	312,56384	42,56653
15	15	384,6	266,41822	224,707232	308,12921	41,71099
16	16	526,3	262,83914	221,970095	303,70818	40,86904
17	17	588,23	259,26006	219,218503	299,30161	40,04155
18	18	285,7	255,68097	216,451542	294,91041	39,22943
19	19	232,56	252,10189	213,668238	290,53555	38,43365
20	20	285,71	248,52281	210,867553	286,17807	37,65526
21	21	370,4	244,94373	208,048389	281,83906	36,89534
22	22	277,8	241,36464	205,209579	277,51971	36,15506
23	23	238,1	237,78556	202,349894	273,22123	35,43567
24	24	212,76	234,20648	199,468034	268,94492	34,73844
25	25	108,6	230,6274	196,56264	264,69215	34,06476
26	26	96,15	227,04831	193,632288	260,46434	33,41603
27	27	144,93	223,46923	190,675496	256,26297	32,79374
28	28	555,55	219,89015	187,690732	252,08957	32,19942
29	29	161,3	216,31107	184,676418	247,94572	31,63465
30	30	256,41	212,73198	181,630946	243,83302	31,10104
31	31	178,6	209,1529	178,552684	239,75312	30,60022
32	32	87,72	205,57382	175,439999	235,70764	30,13382
33	33	50,25	201,99474	172,291268	231,69821	29,70347
34	34	73,53	198,41565	169,104903	227,7264	29,31075
35	35	78,74	194,83657	165,879375	223,79377	28,9572
36	36	21,6	191,25749	162,613231	219,90175	28,64426
37	37	35,46	187,67841	159,305129	216,05168	28,37328
38	38	51,8	184,09932	155,953857	212,24479	28,14547
39	39	68,5	180,52024	152,558359	208,48212	27,96188
40	40	66,22	176,94116	149,117759	204,76456	27,8234
41	41	178,6	173,36208	145,631383	201,09277	27,73069
42	42	344,83	169,78299	142,09877	197,46722	27,68422
43	43	94,34	166,20391	138,519687	193,88813	27,68422
44	44	85,47	162,62483	134,894135	190,35552	27,73069
45	45	243,9	159,04575	131,222347	186,86915	27,8234
46	46	370,4	155,46666	127,504781	183,42855	27,96188
47	47	44,25	151,88758	123,742114	180,03305	28,14547
48	48	39,84	148,3085	119,935222	176,68178	28,37328
49	49	40,65	144,72942	116,085158	173,37367	28,64426
50	50	67,56	141,15033	112,193137	170,10753	28,9572
51	51	92,6	137,57125	108,2605	166,882	29,31075
52	52	166,7	133,99217	104,2887	163,69564	29,70347
53	53	192,3	130,41309	100,279265	160,54691	30,13382
54	54	208,33	126,834	96,2337859	157,43422	30,60022
55	55	135,13	123,25492	92,1538823	154,35596	31,10104
56	56	99,01	119,67584	88,0411898	151,31049	31,63465
57	57	175,44	116,09676	83,8973383	148,29617	32,19942
58	58	137	112,51767	79,7239377	145,31141	32,79374
59	59	80,64	108,93859	75,5225645	142,35462	33,41603
60	60	106,4	105,35951	71,2947518	139,42426	34,06476
61	61	38,76	101,78043	67,0419807	136,51887	34,73844
62	62	73	98,201343	62,7656748	133,63701	35,43567
63	63	55,55	94,62226	58,4671955	130,77733	36,15506
64	64	116,28	91,043178	54,1478399	127,93852	36,89534
65	65	74,07	87,464095	49,8088391	125,11935	37,65526
66	66	73,53	83,885013	45,4513585	122,31867	38,43365
67	67	90,1	80,30593	41,0764981	119,53536	39,22943
68	68	63,3	76,726848	36,685294	116,7684	40,04155
69	69	86,2	73,147765	32,2787205	114,01681	40,86904
70	70	95,24	69,568683	27,8576925	111,27967	41,71099
71	71	71,94	65,9896	23,4230675	108,55613	42,56653
72	72	68,5	62,410518	18,9756491	105,84539	43,43487
73	73	51,02	58,831435	14,5161892	103,14668	44,31525
74	74	61,73	55,252353	10,0453914	100,45931	45,20696
75	75	64,93	51,67327	5,56391346	97,782627	46,10936
76	76	47,62	48,094188	1,07237026	95,116005	47,02182
77	77	50,25	44,515105	-3,4286635	92,458874	47,94377
78	78	16,4	40,936022	-7,9386508	89,810696	48,87467
79	79	46,73	37,35694	-12,45709	87,170969	49,81403
80	80	55,25	33,777857	-16,983511	84,539226	50,76137
81	81	77,52	30,198775	-21,517476	81,915025	51,71625
82	82	99,01	26,619692	-26,058574	79,297959	52,67827
83	83	78,74	23,04061	-30,606422	76,687642	53,64703
84	84	78,12	19,461527	-35,160661	74,083715	54,62219
Сумма	3570	14111

ВЫВОД

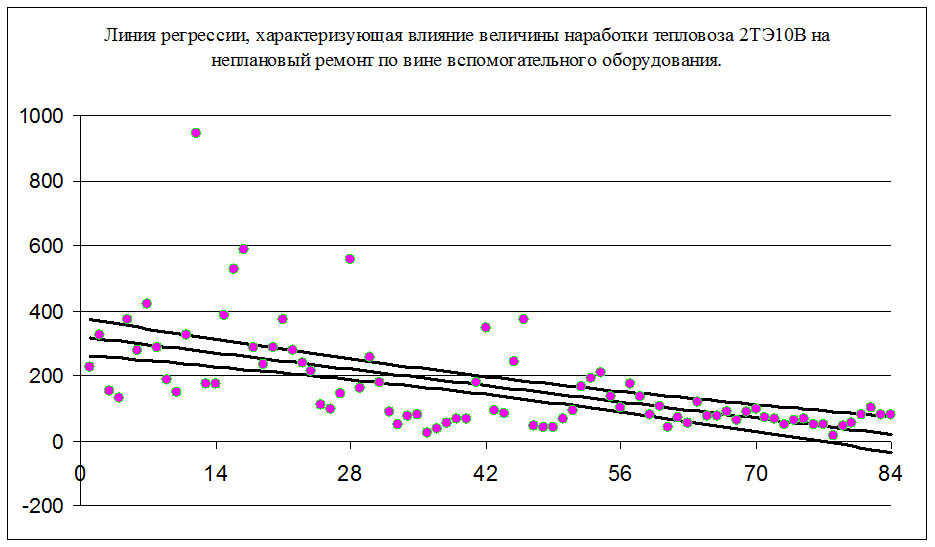
Данные, полученные в результате наблюдений изменения производительности тепловоза 2ТЭ10В в процессе эксплуатации, я представил в виде вариационного ряда. Рассчитал выборочное среднее значение и выборочное среднеквадратичное отклонение. Рассчитал ширину интервала, а затем частоты распределения. Построив гистограмму распределения анализируемой случайной величины, определил вид закона распределения и его параметры при помощи метода моментов. Построил диаграмму рассеивания. Рассчитал соответствующие значения коэффициентов ковариации и корреляции. Получил уравнение линейной функции сглаживания наиболее подходящей к статистическим данным и построил линию регрессии и две линии доверительных границ.

1 2 3

Скачать файл