






220400 Алгебра и геометрия Толстиков А.В.
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 7-22.
2. Общий курс высшей математики. М.: Инфра - М, 2000. с. 72-87
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 16-26.
4. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980, с. 148-156.
1. Векторные пространства
1. Определение числового поля.
Определение 1. Множество Р чисел, содержащее не менее двух чисел, называется числовым полем если для любых двух чисел a, b ÎР выполняются свойства:
1) a + b ÎР;
2) a - b ÎР;
3) ab ÎР;
4) если b¹0, то a / b ÎР.
В дальнейшем мы будем числовое поле называть для краткости просто полем, которое является общим понятием, чем числовое поле. Но все, что говорится в этом параграфе справедливо и для произвольного поля. Элементы поля называются также скалярами.
Примерами числовых полей являются множество R всех действительных чисел, множество Q всех рациональных чисел, но множеств N всех натуральных и множество Z целых чисел не являются числовыми полями.
Упражнение
1. Докажите, что множество Р = {a + b![]() |a, b ÎQ} является числовым полем.
|a, b ÎQ} является числовым полем.
2. Определение векторного пространства.
Определение 2. Непустое множество V элементов вида a, b, c,... называется векторным (или линейным) пространством над полем Р , если
1) на множестве V определена бинарная алгебраическая операция, называемая сложением, и которая любой паре элементов a, b ÎV ставит в соответствие единственный третий элемент из V, обозначаемый a + b и называемый их суммой;
2) определена операция умножения элементов из множества V на числа из поля Р, которая любому элементу a ÎV и любому числу aÎР ставит в соответствие единственный элемент из V , обозначаемый aa и называемый произведением элемента a на число a;
3) эти операции обладают следующими условиями (аксиомами векторного пространства).
1°. Сложение элементов в V ассоциативно, т.е. a + (b + c) =(a + b) + c для любых a, b, c ÎV .
2°. Сложение элементов в V коммутативно, т.е. a + b = b + a для любых a, b ÎV.
3°. Существует нулевой такой элемент 0 ÎV , что для любого a ÎV имеем a + 0 = 0 + a = a.
4°. Для любого a ÎV существует такой элемент -a ÎV, что имеем a + (-a) = (-a) + a = 0 .
5°. Умножение на число дистрибутивно относительно сложения элементов из V , т.е. a(a + b) =aa + ab для любых a, b ÎV и aÎР.
6°. Умножение на число дистрибутивно относительно сложения чисел из Р , т.е. (a + b)a =aa + ba для любых a ÎV и a, bÎР.
7°. (ab)a =a(ba) для любых a ÎV и a, bÎР.
8°. Умножение унарно, т.е. 1a = a для любого a ÎV , где 1 - единица поля Р.
 Элементы
множества V называются векторами, вектор 0 -нулевым
вектором, вектор -a - противоположным вектором для
вектора a. Свойства 1°
- 8° называются аксиомами
векторного пространства.
Элементы
множества V называются векторами, вектор 0 -нулевым
вектором, вектор -a - противоположным вектором для
вектора a. Свойства 1°
- 8° называются аксиомами
векторного пространства.
3. Примеры векторных пространств.
Пример 1. Пространство скаляров. По определению поля следует, что любое поле Р является векторным пространством над самим собой относительно операций сложения и умножения в поле.
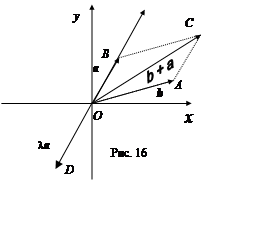
Пример 2. Рассмотрим множество V2 всех радиус векторов координатной плоскости с началом в начале координат, которые складываются по правилу параллелограмма и умножаются на числа поля R как геометрические векторы. Из свойств геометрических векторов следует, что V2 является векторным пространством над полем R.
Пример 3.
Пространство матриц. Пусть ![]() - множество
всех матриц размерности m ´ n
с элементами из поля Р. По определению и свойствам операций сложения
матриц и умножению матрицы на число, это множество является векторным пространством
над полем Р, его называют векторным пространством m´n - матриц над полем Р.
- множество
всех матриц размерности m ´ n
с элементами из поля Р. По определению и свойствам операций сложения
матриц и умножению матрицы на число, это множество является векторным пространством
над полем Р, его называют векторным пространством m´n - матриц над полем Р.
Пример 4. Арифметическое или координатное n-мерное пространство. n - мерным числовым вектором над полем Р называют упорядоченный набор из n чисел поля Р. Числа называются координатами числового вектора. Множество всех n - мерных числовых векторов обозначается символом Рn.
Пусть a=(a1, a2,...,an), b=(b1, b2,...,bn) два n - мерные числовые вектора.
Два n - мерных числовых вектора называются равными, если все соответствующие координаты векторов попарно равны.
Суммой n - мерных числовых векторов называется такой n - мерный числовой вектор, каждая координата которого равна сумме соответствующих координат данных векторов, т.о.
a=(a1+b1,a2+b2,...,an + bn).
Произведением n - мерного числового вектора на число kÎP называется такой n - мерный числовой вектор, каждая координата которого равна произведению числа k на соответствующую координату данного вектора, т.о.
ka = (ka1, ka2,...,kan).
Заметим, что n - мерные числовые вектора являются матрицами размерности 1´n и операции сложение и умножение на число совпадают с матричными операциями. Поэтому множество Рn является векторным пространством над полем Р. Оно называется n-мерным арифметическим или координатным пространством, или пространством строк длины n над полем Р.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.