220400 Алгебра и геометрия Толстиков А.В.
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 197, с. 7-22.
2. Общий курс высшей математики. М.: Инфра - М, 2000. с. 72-87
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 16-26.
4. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980, с. 148-156.
1. Скалярное произведение
1. Числовая
ось. Прямая l, на которой выбрано начало
отсчета - точка O, положительное направление и
единичный отрезок, называется числовой осью. Числовую ось можно также
задать точкой O и вектором e единичной длины, параллельным оси. Вектор e называется ортом
числовой оси. В качестве единичного отрезка выбирается конец вектора ![]() = e, отложенного от точки O.
= e, отложенного от точки O.
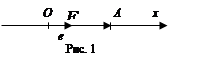 Координатой
точки A на числовой оси называется координата x вектора
Координатой
точки A на числовой оси называется координата x вектора ![]() в
базисе e:
в
базисе e: ![]() = xe. Координату
точки обозначаем символом A(x).
Координаты точки устанавливают биективное соответствие между множеством всех
точек прямой и множеством R действительных
чисел.
= xe. Координату
точки обозначаем символом A(x).
Координаты точки устанавливают биективное соответствие между множеством всех
точек прямой и множеством R действительных
чисел.
2. Угол между векторами.
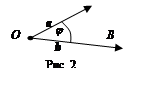 Определение
1. Углом j между
векторами a, b называется угол между
направленными отрезками
Определение
1. Углом j между
векторами a, b называется угол между
направленными отрезками ![]() ,
,
![]() , которыми
изображаются данные вектора и которые отложены из одной точки.
, которыми
изображаются данные вектора и которые отложены из одной точки.
Угол между векторами обозначаем символом Ð(a, b).
Если вектора a, b коллинеарны, то угол между векторами считается равным нулю. Если хотя бы один из векторов a или b нулевой, угол между векторами a и b неопределен.
Угол меду векторами в пространстве не ориентированный. Угол меду векторами на плоскости ориентированный. Угол считается положительным, если поворот от первого вектора ко второму совершается в направлении против часовой стрелки. В противном случае угол считается отрицательным.
Нетрудно доказать, что угол меду векторами не зависит от точки O.
3. Векторная проекция вектора на прямую.
Определение 2. Проекцией точки A на прямую l называется основание A¢ перпендикуляра AA¢, опущенного из точки A на прямую l.
Определение
3. Проекцией направленного отрезка ![]() на прямую l называется направленный отрезок
на прямую l называется направленный отрезок
![]() , где A¢
и B¢ соответственно проекции точек A
и B на прямую l.
, где A¢
и B¢ соответственно проекции точек A
и B на прямую l.
Определение 4. Проекцией (векторной проекцией) вектора a на прямую l называется вектор, изображаемый проекцией направленного отрезок, который изображает данный вектор a.
Векторная проекция вектора a на прямую l изображается символом прl a.
Теорема 1. Векторная проекция прl a не зависит от направленного отрезка, которым изображается данный вектор a.
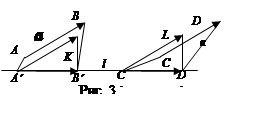 Доказательство.
Пусть вектор a изображается направленным отрезком
Доказательство.
Пусть вектор a изображается направленным отрезком ![]() ,
, ![]() проекция
проекция ![]() на прямую l (см. рис. 21).Точки A¢ и B¢ можно получить, проведя
через точки A и B
плоскости перпендикулярные прямой l. От точки A¢
отложим вектор a: a =
на прямую l (см. рис. 21).Точки A¢ и B¢ можно получить, проведя
через точки A и B
плоскости перпендикулярные прямой l. От точки A¢
отложим вектор a: a =![]() . Четырехугольник A¢ABK - прямоугольник. Так как A¢A ^ l, то BK ^ l и плоскость B¢BK ^ l. Тогда BK ^ l и точка B¢
- проекция точки K. Таким образом,
направленные отрезки
. Четырехугольник A¢ABK - прямоугольник. Так как A¢A ^ l, то BK ^ l и плоскость B¢BK ^ l. Тогда BK ^ l и точка B¢
- проекция точки K. Таким образом,
направленные отрезки ![]() и
и
![]() имеют одну и
туже проекцию
имеют одну и
туже проекцию![]() .
.
Пусть вектор a
изображается также направленным отрезком ![]() ,
, ![]() проекция
проекция ![]() на прямую l.От точки С¢ отложим вектор a: a
=
на прямую l.От точки С¢ отложим вектор a: a
=![]() . Направленные
отрезки
. Направленные
отрезки ![]() и
и ![]() имеют одну и туже проекцию
имеют одну и туже проекцию
![]() . Докажем, что
. Докажем, что
![]() =
=![]() .
.
Так как
треугольники A¢B¢K и C¢D¢L
равны, то A¢B¢ = C¢D¢. Так как лучи A¢ B¢ и C¢ D¢ сонаправлены,
то ![]() =
=![]() .
.
Теорема 2. Для любой прямой l, для любых векторов a, b и для любого числа l справедливы следующие свойства:
1) прl (a + b) = прl a + прl b;
2) прl (l a) = l прl a.
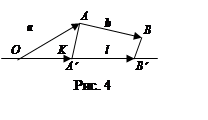 Доказательство.
Возьмем точку O на прямой lи построим сумму
векторов a, b: a + b =
Доказательство.
Возьмем точку O на прямой lи построим сумму
векторов a, b: a + b =![]() =
= ![]() (см. рис. 22). Пусть A¢ и B¢ проекции точек A и B
на прямую l. Тогда
(см. рис. 22). Пусть A¢ и B¢ проекции точек A и B
на прямую l. Тогда
прl (a + b)
=![]() =
=
= прl a + прl b.
Свойство 2 докажите самостоятельно ( рассмотрите три случая l =0, l > 0, l < 0).
4. Скалярная проекция вектора.
Определение 5. Пусть l числовая ось, e - орт числовой оси. Проекцией (скалярной проекцией) вектора a на ось l называется число равное координате вектора прl a в базисе e.
Проекция вектора a на ось l изображается символом прl a, или прe a . По определению проекции вектора имеем
прl a = прe a×e. (1)
Проекцию вектора a на ось l можно задать произвольным вектором b, сонаправленным с вектором e. В этом случае ее также обозначают символом прb a и называют проекцией вектора a на вектор b. И по определению имеем прb a = прe a.
В силу однозначности разложения вектора по векторам базиса проекция по этой формуле определяется однозначно. Из этой же формулы следует, что
прl a = прe a =±|прl a|, где стоит знак "+", если прl a e , знак "-", если прl a ¯e.
Теорема 3. Для любых векторов a, b, c и для любого числа l справедливы следующие свойства:
1) прc (a + b) = прc a + прc b;
2) прc (l a) = l прc a,
3) прc a = |a| cos j, где j = Ð( a, c).
Доказательство. В силу определения достаточно доказать теорему для того случая когда c - орт числовой оси l. По теореме 2 и формуле (1) получаем
прl(a + b) = прe (a + b) ×e,
прla + прlb = прea×e + прeb×e = (прea + прeb)×e.
В силу однозначности разложения вектора по векторам базиса получаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.