Обратная матрица для матрицы А существует тогда и только тогда, когда detA¹0, при этом обратная матрица находится единственным образом.
Если
определитель матрицы А не равен нулю, то матрица А называется невырожденной
или неособенной матрице. В силу теоремы 5 A-1
существует тогда и только тогда, когда матриц А невырожденная.![]()
Доказательство.
1. Необходимость. Пусть для матрицы А существует обратная матрица
A-1. Тогда по определению А× A-1=Е. Переходя к определителям и
пользуясь теоремой 5 получим: ![]() . Отсюда
detA=|А|¹0.
Необходимость доказана.
. Отсюда
detA=|А|¹0.
Необходимость доказана.
2. Достаточность. Пусть дана
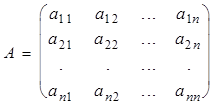 , |А|=d¹0.
, |А|=d¹0.
Построим матрицу A-1 следующим образом. Заменим каждый элемент матрицы А его алгебрамческим дополнением и получим матрицу
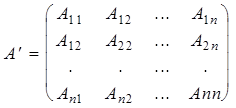 .
.
Полученную матрицу транспонируем и находим матрицу
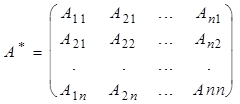
(эта матрицы называется присоединененной или взаимной матрице к матрице А). Докажем тогда, что
![]() .
(4)
.
(4)
Для этого докажем равенства (3).
![]()
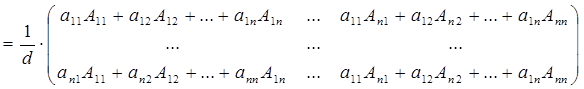 .
.
По следствию из теоремы о разложении определителя по элементам ряда
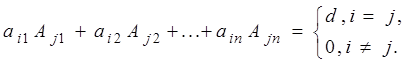
Тогда
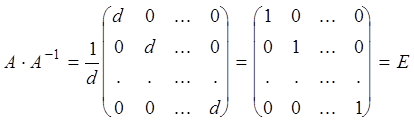 .
.
Аналогично доказывается, что A-1×A=E.
Доказывая
единственность обратной матрицы, допустим противное, что матрица А имеет
две обратные матрицы ![]() . Тогда по
определению и свойствам умножения матриц имеем
. Тогда по
определению и свойствам умножения матриц имеем
![]() .
.
Теорема доказана.
Доказательство этой теоремы дает алгоритм для вычисления обратной матрицы.
Пример 3. Найти обратную матрицу для матрицы
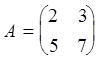 .
.
Вычислим определитель матрицы A,
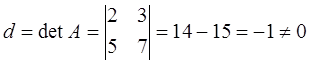 ,
,
Тогда обратная матрица существует. Вычислим алгебраические дополнения матрицы А и составим матрицу из алгебраических дополнений.
![]()
![]() .
.
Транспонируем полученную матрицу:
![]() .
.
Отсюда
![]() .
.
6. Матричные уравнения и системы линейных уравнений. Пусть А квадратная матрица порядка n, матрица В имеет n строк, матрица С имеет n столбцов. Рассмотрим следующие матричные уравнения:
![]() , (5)
, (5)
и
![]() , (6)
, (6)
где X и Y неизвестные матрицы.
Теорема 6. Если detA¹0 , то каждое из уравнений (5) и (6) разрешимо, имеет единственное решение, решения находятся соответствеено по формулам:
![]() (7)
(7)
и
![]() . (8)
. (8)
Доказательство. Рассмотрим уравнение (5), так как уравнение (6) рассматривается аналогично. Покажем сначала, что если Х0 решение уравнения (5) то оно находится по формуле (7). Действительно, имеем равенство А×Х0=В. Умножаем обе части этого равенства на А-1 и последовательно находим
А-1×(А×Х0)=А-1×В, (А-1×А)×Х0=А-1×В, Е×Х0= А-1×В, Х0=А-1×В.
Покажем теперь, что матрица, найденная по формуле (7) является решением уравнения (5):
А×Х=А×(А-1×В)=(А×А-1)×В=Е×В=В.
Докажем, что решение уравнения (5) единственно. Действительно, если Х1 и Х2 решения уравнения (5) то выполняются равенства:
А×Х1=В и А×Х2 =В.
Приравнивая левые части этих равенств последовательно получаем
А×Х1=А×Х2, А-1×( А×Х1)=А-1×(А×Х2), ( А-1×А)×Х1=(А-1×А)×Х2, Е×Х1=Е×Х2, Х1=Х2.
Теорема доказана.
Запишем систему линейных уравнений, воспользовавшись определениеми равенства и умножения матриц.
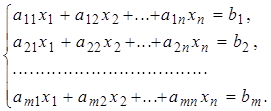 (9)
(9)
Система (9) равносильна матричному равенству
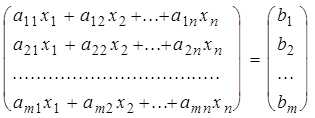
или
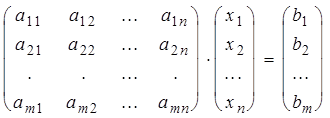 ,
,
АХ=В, (10)
где А - матрица систем, В - столбец свободных членов, Х - столбец неизвестных. Отметим, что система (9) равносильна матричному уравнению (10). Тогда по теоремы 6 получим следующее предложение.
Теорема 7. Пусть в системе линейных уравнений (9) число уравнений равно числу неизвестных (m=n) и d=detA¹0. Тогда система линейных уравнений (9) имеет единственное рашение, которое находится по формуле
Х=А-1×В. (11)
По формуле (11) и способу вычисления обратной матрицы получаем
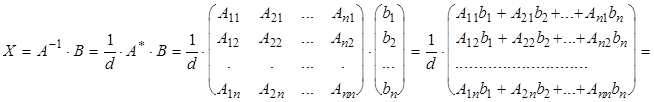
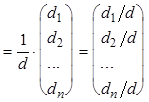 , где di
получается из d заменой i-го столбца столбцом свободных членов.
Отсюда получаем найденные ранее формулы Крамера:
, где di
получается из d заменой i-го столбца столбцом свободных членов.
Отсюда получаем найденные ранее формулы Крамера:
![]() .
.
7. Элементарные матрицы.
Определение 8. Элементарными матрицам называются такие матрицы, которые получаются с помощью одного элементарного преобразования из единичной матрицы.
Таким образом элементарные матрицы получаются из единичной матрицы с помощью следующих элементарных преобразований: 1) перестановка двух строк (i-й и j-й) местами; 2) умножение какой-нибудь строки (i-й) на число с¹0; 3) прибавление к какой-нибудь строке (i-й) другой строки (j-й), умноженной на число с. Они имеют соответственно следующий вид (первой указана единичная матрица, из которой получены следующие за ней элементарные матрицы, в каждой матрице выделены i-я и j-я строки и i-й и j-й столбцы):
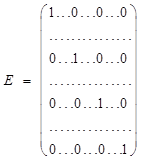 ,
,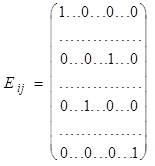 ,
,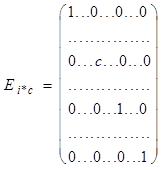 ,
,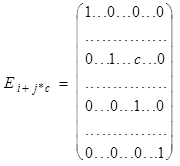 .
.
Элементарные матрицы обладют следующими свойствами.
1. Определители элементарных матриц не равны нулю и
![]() .
.
2. Элементарные матрицы обратимы и обратные матрицы для элементарных матриц являются элементарными матрицами:
![]() .
.
3. Если матрицу А порядка n умножить слева на элементарную матрицу порядка n, то с матрицей А произойдет элементарное преобразование с помощью которого элементарная матрица получена из единичной матрицы.
Свойство 1 следует из свойств определителя, свойство 2 доказывается
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.