Евклидовы пространства. Неравенство Коши-Буняковского. Норма вектора и ее свойства. Матрица Грама скалярного произведения и ее свойства

220400                   Алгебра и геометрия                    Толстиков А.В.

Лекции 12. Евклидовы пространства.

План

1.  Скалярное произведение в векторных пространствах. Определение, простейшие свойства и примеры евклидова пространства.

2.  Неравенство Коши - Буняковского. Норма вектора и ее свойства.

3.  Матрица Грама скалярного произведения и ее свойства.

4.  Ортогональная система векторов. Процесс ортогонализации. Ортогональный и ортонормированный базис.

5.  Ортогональное дополнение.

Рекомендуемая литература

1.  Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.

2.  Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997.

3.  Воеводин В.В. Линейная алгебра.. М.: Наука 1980.

4.  Сборник задач по для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П.. М.: Наука, 1981.

5.  Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах. М.: Физматлит, 2001.

6.  Воеводин В.В. Линейная алгебра. М.: Наука, 1980.

1.  Скалярное произведение в векторных пространствах. Определение, простейшие свойства и примеры евклидова пространства. Пусть V  векторное пространство над полем действительных чисел R

Определение 1. Отображение множества V´V в R, которое каждой упорядоченной паре (a, b) векторовa, b из V ставит в соответствие единственное число изR, обозначаемое (a, b) или ab,называется скалярным произведение, если оно обладает свойствами:

1)  (" aÎV) aa ³ 0; aa = 0Û a = 0;

2)  (" a, b ÎV) ab =ba;

3)  (" a, b, c ÎV) a(b + c) = ab + ac;

4)  (" a, b ÎV) (" aÎR)(aa)b =a(ab).

Определение 2. Евклидовым пространством называется векторное пространство над полем R, на котором определено скалярное произведение векторов. Обозначаем n - мерное евклидово пространство символом E_n.

Свойство 1. 0×a = 0.

Доказательство. По свойству векторного пространства 0×b = 0 для любого b ÎV . Отсюда по определению 1 и свойствам поля получим:

а×0 = а×(0×b)= (0×b)×а = 0×(b×а) = 0.

Свойство 2. (-a)b = -ab.

Доказательство. По свойству векторного пространства (-1)×a = -a для любого a ÎV . Отсюда по определению 1 и свойствам поля получим:

(-a)× b  = ((-1)a)×b= (-1)(а×b)= -а×b = 0.

Свойство 3.  .

Доказательство.  Действительно, по определению при k = 2 имеем:

(a₁a₁ + a₂a₂)b  = (a₁a₁)×b + (a₂a₂)×b = a₁(a₁×b) + a₂(a₂×b), а в общем случае равенство доказывается методом математической индукции по k. 

Пример 1. Покажем, что в любом n-мерном векторном пространстве V можно ввести скалярное произведение. Пусть v₁ ,v₂ ,... v_n - базис V и  произвольные векторы a, b ÎV разложены по базису.

a = a₁v₁ + a₂v₂ +...+ a_nv_n , b = b₁v₁ + b₂v₂ +...+ b_nv_n.

Определим скалярное произведение по формуле:

аb = a₁b₁+ a₂b₂+ ... + a_kb_k.

Тогда аb Î Р и определено однозначно. Условие 1° следует из коммутативности умножения чисел в поле Р.  Проверяя условие 2° рассмотрим еще вектор с = g₁v₁ + g₂v₂ +...+ g_nv_n. Тогда

a  +  b = (a₁ + b₁)v₁ + (a₂ + b_n)v₂ +...+ (a_n +  b_n)v_n.

(a + b)c = (a₁ + b₁)g₁ +(a₂ + b₂)g₂ + ...+ (a_k + b_k)g_k  =

= (a₁g₁ +a₂g₂ + ...+ a_kg_k) + (b₁g₁ +b₂g₂ + ...+ b_kg_k) = аb + ac .

Условие 3° проверяется аналогично.

Пример 2. Пространство геометрических векторов R₃ является евклидовым пространством, если в нем скалярное произведение векторов определено по формуле:  , где  - длины векторов ,j - угол между этими векторами. Проверка условий в определениях 1 , 4 производилась в курсе аналитической геометрии.

Пример 3. Арифметическое n-мерном Rⁿнад полем R является евклидовым, если в нем определить скалярное произведение по формуле:

аb = a₁b₁+ a₂b₂+ ... + a_kb_k, где a = (a₁, a₂, ..., a_n),  b = (b₁, b₂, ..., b_n) Î Rⁿ. Проверку условий в определениях 1 , 4 произведите самостоятельно.

Пример 4. Любое n-мерном векторном пространстве V над полем R является евклидовым, если в нем определить скалярное произведение по формуле:

аb = a₁b₁+ a₂b₂+ ... + a_kb_k, где a = a₁v₁ + a₂v₂ +...+ a_nv_n , b = b₁v₁ + b₂v₂ +...+ b_nv_n разложения векторов a, b ÎV  по некоторому базису v₁ ,v₂ ,... v_n пространства V . Так как ранее (пример 1) было доказано, что это скалярное произведение, то осталось проверить, что aa  > 0 для любого a Î V, a ¹ 0. Действительно, если a ¹ 0, то хотя одна из координат a₁, a₂, ..., a_n вектора a неравна нулю и aa = a₁² + + a₂² +...+ a_n² > 0.

Пример 5. Пространство С[a,b] непрерывных на отрезке [a,b] фуекций явлется евклидовым пространство, если вввести на нем скалярное произведение по формуле:

.                                                                       (6)

Так как определенный интеграл от непрерывных функций существует, определен однозначно и принадлежит R, то проверим условия в определениях 1 и 5 используя свойства опрераций над функциями и свойства определенного интеграла.

1° =.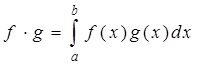

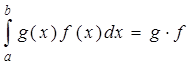2° .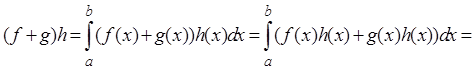

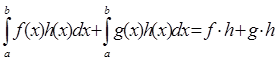3°  .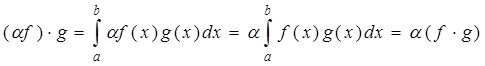

4° 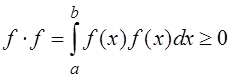 и если f ¹ 0, то f × f > 0.

2.  Неравенство Коши - Буняковского. Норма вектора и ее свойства.

Определение 1. Пусть E - евклидово пространство. Длиной или нормой вектора a Î E называется величина  .

Определение 2. Косинусом угла между векторами a и b из E называется величина .

Tеорема 1. Для любых векторов и чисел справедливы свойства:

1)  ;

2)  ;