Евклидовы пространства. Неравенство Коши-Буняковского. Норма вектора и ее свойства. Матрица Грама скалярного произведения и ее свойства, страница 2

3)  или   (неравенство Коши Буняковского);

4)   (неравенство треугольника).

Доказательство. 1. Следует из определения  скалярного произведения в евклидовом пространстве.

2. .

3.  Если a = 0, то имеем. Пусть a ¹ 0. По определению евклидова пространства, для любого  числа l имеем . Тогда для любого l Î R значение квадратного трехчлена. Так как a² > 0, то тогда дискриминант . Отсюда получаем.

4. 4. Так как

|a + b|² = (a + b)² = (a + b)×(a + b) =  a² + 2(ab) + b² = |a|² + |b|² + 2(ab) =

 = (|a|+ |b|)² - 2|a||b| + 2(ab) = (|a|+ |b|)² - 2(|a||b| -ab), то по неравенству Коши-Буняковского |a + b|² £  (|a|+ |b|)². Отсюда |a + b| £ £ |a| + |b|. 

3. Матрица Грама скалярного произведения и ее свойства.

Определение 1. Пусть dim E = n. Матрицей Грама скалярного произведения системы векторов a₁, a₂, ..., a_n из E называется определитель

.

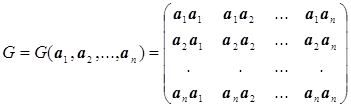Определитель матрицы Грама называется определителем Грама.

Пусть система векторов a₁, a₂, ..., a_n линейно выражается через систему векторов b₁, b₂, ..., b_n

.

Тогда

, по определению произведения двух матриц получаем

.

Если через T= обозначим матрицу перехода от первой системы векторов ко второй, то получаем формулу

G = T^t G' T ,                                                                                      (1)

где G и G' определители Грама систем векторов a₁, a₂, ..., a_n и b₁, b₂, ..., b_n соответственно.

Теорема 1.При перестановке векторов определитель Грама не меняется.

Доказательство. При перестановке двух векторов в системе a₁, a₂ , ..., a_k в определителе Грама переставляются сразу две строки и два столбца и при этом абсолютная величина и знак определителя сохраняются. Так как любую перестановку свекторов можно свести к последовательному выполнению перестановок пар векторов, то при перестановке векторов определитель Грама не меняется.

Теорема 2. Система векторов линейно зависима тогда и только тогда, когда ее определитель Грама равен нулю. Если система векторов линейно независима, то ее определитель Грама больше нуля.

Доказательство. Если векторы линейно зависимы, то хотя бы один из векторов a₁, a₂ , ..., a_k линейная комбинация остальных векторов системы

.

Тогда

и одна из строк определителя Грама линейная комбинация остальных строк определителя. Поэтому определитель Грама. равен нулю.

Пусть система векторов a₁, a₂ , ..., a_k линейно независима. Применим к ней процесс ортоганализации и перейдем к ей эквивалентной ортогональной системе векторов b₁, b₂, ..., b_n. Пусть  матрица перехода от первой системы векторов ко второй. Тогда имеет место формула

G = T^t G T ,                                                                                      (1)

где G и G' определители Грама систем векторов a₁, a₂, ..., a_n и b₁, b₂, ..., b_n соответственно. Для ортогональной системы векторов матрица Грама равна

.

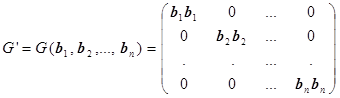Так как b_i b_i > 0, то последний определитель больше нуля. Поэтому

detG = det(T^t G T) = detT^t× detG'× detT = (detT^t)²× detG' > 0.

4. Ортогональная система векторов. Процесс ортогонализации. Ортогональный и ортонормированный базис.

Определение 1. Два вектора a и b из E называются ортогональными, если их скалярное произведение равно нулю.

Определение 2. Система ненулевых векторов b₁, b₂, ..., b_m называется ортогональной системой векторов, если различные векторы этой системы попарно ортогональны: b_ib_j = 0 (i, j = 1, 2,…, m; i ¹ j).

Теорема 1.Ортогональная система векторов линейно независима.

Доказательство. Пусть a₁, a₂ , ..., a_k -ортогональная система ненулевых векторов из V. Доказывая линейную независимость системы a₁, a₂ , ..., a_k  допустим, что выполняется равенство: