Евклидовы пространства. Неравенство Коши-Буняковского. Норма вектора и ее свойства. Матрица Грама скалярного произведения и ее свойства, страница 4

Доказательство.  Скалярное произведение в евклидовом пространстве невырожденное. Поэтому по следствю теоремы 2 Е_n обладает ортогональным базисом b₁, b₂ , ..., b_n . Тогда легко показать, что система векторов

е₁ =  , e₂  =    , ..., е_n  =   

- линейно независима. Она образует ортонормированный базис Е_n. Действительно,

е_i×e_j =, если i, j = 1, 2, ...,n, i ¹ j;

е_i×e_i =,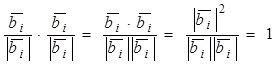

i = 1, 2, ...,n. 

Пример 1. Ортогонализовать систему векторов  a₁ =  (1, 0,  0)  ,   a₂ = =(-1,1, 0), a₃ = (4, -2, 2) (скалярное произведение определено в примере 1). Пусть b₁ = (1, 0, 0).

По формуле (2)   b₂ = b₁b₁+ a₂,  где коэффициент  b₁ находим по формуле (3):  b₁= (-a₂b₁)/(b₁b₁) = -(-1)/1 = 1. Тогда b₂ = b₁+ a₂= (0, 1, 0).

По формуле (2)  b₃ = b₁b₁ + b₂b₂ + a₃ ,  где коэффициенты  b₁ , b₂  находим по формуле (3):  b₁= (-a₃b₁)/(b₁b₁) = -4/1 = -4. b₂= (-a₃b₂)/(b₂b₂) = -(-2)/1 = = 2. Тогда b₂ = -4b₁ + 2b₂ + a₃= (0, 0, 2).  и ищем  v₂ = (-1, 1, 0), v₃ = (4, -2, 2)   линейно независима  и образует базис пространства R³

Ортогональная система векторов a₁ = (1,0,0), a₂ = (0,1,0), a₃ = (0,0,2).

.5.   Ортогональное дополнение.

Определение 1. Пусть  L - подпространство евклидова пространства E. Ортогональным дополнением L называется множество L^{^} всех векторов из E ортогональных каждому вектору из L: L^{^} = { bÎE | для любого вектора a Î L имеем b a = 0 }.

Теорема 1.. Для любого подпространства L из E ортогональное дополнение L^{^}  есть  подпространство из E.

Доказательство. По определению L^{^} Ê E. Так как для любого вектора a Î L имеем 0 a = 0, то 0 Î L^{^} и L^{^} ¹ Æ.

Проверим условия, входящие в определение подпространства.

1)  Пусть b, c Î L^{^}, тогда для любого a Î L имеем (b + c) a = b a + c a = 0+ 0 = 0, и b + c Î L^{^}.

2)  Пусть b Î L^{^} , lÎR, тогда для любого a Î L имеем (lb) a =l(b a) =l 0 = 0, и lb Î L^{^}.

Отсюда по определению L^{^} - подпространство из E. 

Теорема 2.  Для любого подпространства L из E L ÇL^{^} = {0}.

Доказать самостоятельно.

Теорема 3.. Если E - конечномерное евклидово пространство, то E прямая сумма L и L^{^} : E= L Å L^{^}.

Доказательство. Если L = {0}, то L^{^} = E. Если L ¹ {0}, то подпространство L имеет базис e₁, e₂,…, e_k, который в силу теоремы предыдущего параграфа, можно считать ортогональным.  По теореме о базисах этот базис можно дополнить до базиса пространства E и полученный базис ортогонолизовать. Получим ортогональный базис e₁, e₂,…, e_k, e_{k +1},…, e_n пространства E. Тогда любой вектор a Î E представляется единственным образом в виде:

a = a₁e₁ + a₂e₂ +…+ a_ke_k + a _{k +1}e_{k +1} +…+ a _n e_n = b + c; b Î L, c Î L^{^}.

Отсюда и теоремы 2 по определению прямой суммы следует, что E = L Å L^{^}. 

Следствие. Если E - конечномерное евклидово пространство, то dim E = dim L + dim L^{^}.

Теорема 4. Пусть V - конечномерное векторное пространство с невырожденным скалярным призведением, L, L₁, L₂- подпространства из V. Тогда справедливы следующие свойства:

1°  (L^{^})^{^} = L;

2°  если L₁ Í L₂ , то L₁^{^} Ê L₂^{^};

3°  (L₁ + L₂)^{^} = L₁^{^} Ç L₂^{^};

4°  (L₁ Ç L₂)^{^} = L₁^{^} + L₂^{^}.

Доказательство. 1°  Eсли a Î L , то ab =0 для любого b Î  L^{^}. Поэтому a Î L^{^} и  L Í (L^{^})^{^}. Докажем, что (L^{^})^{^} Í L и тогда получим (L^{^})^{^} = L.

Пусть a Î (L^{^})^{^} . Так как (L^{^})^{^} Í V и по теореме 4 V = L Å L^{^}, то a = b  + b¢ ,   где  b Î L ,  b¢ Î L^{^} . Поэтому bb¢ = 0. Так как a Î (L^{^})^{^} , то ab¢ = 0. Отсюда b¢b¢  = (a - b)b¢ = ab  - ab¢  = 0 + 0 = 0. В силу невырожденности скалярного произведения b¢  = 0 и a = b  Î L . Свойство доказано.

Свойства 2° - 4° рекомендуется доказать читателю самостоятельно.