Плоскость и прямая в пространстве. Взаимное расположение прямых и плоскостей. Углы между прямыми

Таким образом, M(x,y,z)Îs тогда и только тогда, когда f(x,y,z)= 0.

Если f(x,y,z) многочлен степени n, то поверхность s называется поверхность n - го порядка.

Основными задачами аналитической геометрии в пространстве являются следующие задачи:

1)  по определению поверхности составить ее уравнение в заданной пространственной системе координат;

2)  по уравнению поверхности изучить ее свойства,  установить вид поверхности и изобразить ее.

Определение 2. Сферой с центром в точке C радиуса r называется геометрическое место всех точек пространства, для каждой из которых расстояние до точки C равно r.

Обозначим сферу с центром в точке C  радиуса символом S(C,r).

Выведем уравнение сферы в данной прямоугольной системе координат Oxyz. Пусть C(x₀,y₀,z₀). По определению сферы точка M(x,y,z) принадлежит сфере с центром в точке C радиуса r тогда и только тогда, когда

|CM| = r.                                            (2)

По формуле расстояния между двумя точками равенство (2) можно представить в виде:

.

Возведем в квадрат обе части полученного уравнения и находим уравнение сферы:

,           (3)

которое равносильное первоначальному.

Если центр сферы совпадает с началом координат, то уравнение (3) принимает вид:

.                                       (4)

С помощью систем уравнений и неравенств могут быть в пространстве определены различные пространственные тела.

Определение 3. Шаром с центром в точке C радиусаr называется геометрическое место всех точек пространства, для каждой из которых расстояние до точки C не больше r. 

Шар с центром в точке C(x₀,y₀,z₀) радиуса r задается неравенством

.

2.  Различные уравнения плоскости

Пусть в пространстве R ³ задана прямоугольная система координат Oxyz.

Определение 1. Нормальным вектором плоскости a называется любой ненулевой вектор n перпендикулярный плоскости a.

Пусть n = (A,B,C) ¹ 0, -нормальный  вектор плоскости a, M₀(x₀,y₀,z₀)- точка, принадлежащая плоскости a. Пусть M(x,y,z), произвольная точка пространства,

.

Тогда точка M принадлежит плоскости a тогда и только тогда, когда векторы  и nортогональны. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, Последнее в ортонормированном базисе можно записать в виде:

A(x - x₀) + B(y - y₀) +C(z - z₀) = 0 .                                                                         (1)

Таким образом, получаем уравнение плоскости, проходящей через точку и перпендикулярной вектору n = (A,B,C) ¹ 0.

Рассмотрим произвольное уравнение первого порядка

Ax  + By + Cz + D = 0,                                                                                    (2)

где коэффициенты одновременно не равны нулю, т.е. A²+ B²+ C² ¹ 0.

Теорема 1. Любую плоскость в произвольной аффинной системе координат можно задать уравнением (1) первого порядка и обратно любое уравнение (1) первого порядка в аффинной системе координат определяет плоскость.

Доказательство. Достаточно доказать теорему для прямоугольной системы координат. Любую плоскость в прямоугольной системе координат можно задать ее нормальным вектором n = (A,B,C) ¹ 0 и точкой M₀(x₀,y₀,z₀), принадлежащей плоскости. Уравнение этой плоскости выведено в §2.2 и имеет вид:

A(x - x₀) + B(y - y₀) +C(z - z₀) = 0.

отсюда получаем

Ax + By  +Cz +(-Ax₀ - By₀ - Cz₀)= 0,

Ax + By  +Cz + D= 0, где D = -Ax₀ - By₀ - Cz₀. Так (A,B,C) ¹ 0, то A²+ B²+ C² ¹ 0 и любая плоскость есть поверхность первого порядка.

Обратно, пусть некоторая поверхность в пространстве определена уравнением (1). Так как не все коэффициенты равны нулю, то уравнение (1) имеет решение (x₀,y₀,z₀). Тогда

Ax₀ + By₀ + Cz₀ + D = 0,                                                               (3)

и точка M₀(x₀,y₀,z₀) принадлежит поверхности.  Вычитая почленно из уравнения (1) равенство (2), получим уравнение

A(x - x₀) + B(y - y₀) +C(z - z₀) = 0,

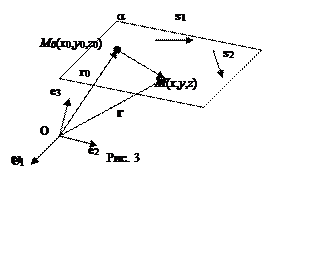равносильное уравнению (1). Это уравнение в силу §2.2, определяет плоскость, проходящую через точку M₀(x₀,y₀,z₀), перпендикулярную вектору n = (A,B,C).

Определение 2. Направляющими векторами плоскости a называется пара неколлинеарных векторов s₁ и s₂ параллельных плоскости a.

Пусть s₁ = (m₁,k₁,l₁), s₂ = (m₂,k₂,l₂)  -направляющие вектора плоскости a, M₀(x₀,y₀,z₀)- точка, принадлежащая плоскости a. Пусть M(x,y,z), произвольная точка пространства,

.

Тогда точка M принадлежит плоскости a тогда и только тогда, когда