Курс: Алгебра и геометрия
Лекция 2
Определители
План
1. Перестановки и их четность.
2. Подстановки и их четность
3. Определение определителя.
4. Свойства определителей.
5. Теорема о разложении определителя по элементам ряда.
6. Вычисление определителей.
7. Правило Крамера.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 7-22.
2. Общий курс высшей математики. М.: Инфра - М, 2000. с. 72-87
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 16-26.
4. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980, с. 148-156.
1. Перестановки подстановки и их четность.
Определение
1. Перестановкой из n различных элементов или n - перестановкой
называется любое упорядоченное расположение этих элементов. Обозначаем n
- перестановки символом ![]() , где
, где
![]() различные
элементы n-элементного множества M.
различные
элементы n-элементного множества M.
Теорема 1.![]() Число всех
перестановок из n различных элементов равно
Число всех
перестановок из n различных элементов равно ![]() .
.
Доказательство.
В перестановке ![]() элемент
элемент ![]() из множества M можно
выбрать n различными способами. Элемент
из множества M можно
выбрать n различными способами. Элемент ![]() из
оставшихся элементов можно выбрать n-1 способами, элемент
из
оставшихся элементов можно выбрать n-1 способами, элемент ![]() - n-2 способами и т.д.
. Наконец элемент
- n-2 способами и т.д.
. Наконец элемент ![]() можно выбрать одним
способом. Тогда по правилу произведения перестановку
можно выбрать одним
способом. Тогда по правилу произведения перестановку ![]() можно составить
можно составить ![]() способами. Теорем доказана.
способами. Теорем доказана.
В дальнейшем
рассматриваем n - перестановки из элементов множества ![]() .
.
Определение
2. Говорят, что элементы i и j в перестановке ![]() образуют инверсию
(беспорядок), если
образуют инверсию
(беспорядок), если ![]() и i стоит
впереди j .
и i стоит
впереди j .
Число всех
инверсий в перестановок ![]() обозначаем
символом
обозначаем
символом ![]() .
.
Определение 3. Перестановка называется четной, если число всех инверсий в перестановке четное, перестановка называется нечетной, если число всех инверсий в перестановке нечетное.
Пример 1. В
перестановке ![]() =(1,5,4,2,3) элементы 5 и 4 ,
5 и 2, 5 и 3, 4 и 2, 4 и 3 образуют инверсии. Поэтому
=(1,5,4,2,3) элементы 5 и 4 ,
5 и 2, 5 и 3, 4 и 2, 4 и 3 образуют инверсии. Поэтому ![]() и перестановка
и перестановка ![]() нечетная.
нечетная.
Пример 2. Для n=2
имеется две перестановки:![]() При этом
перестановка (1,2) - четная, а перестановка (2,1) нечетная.
При этом
перестановка (1,2) - четная, а перестановка (2,1) нечетная.
Пример 3. Для n=2 имеется 6 перестановок. При этом три перестановки (1,2,3), (3,1,2), (2,3,1) четные и три перестановки (1,3,2), (2,1,3), (3,2,1) нечетные.
Определение 4. Транспозицией перестановки называется такое ее преобразование при, при котором два ее элемента переставляются местами, а остальные остаются на своих местах.
Теорема 2. При любой транспозиции перестановки ее четность меняется на противоположную.
Доказательство. Рассмотрим два случая.
1. Производится
транспозиция соседних элементов i и j . Пусть исходная
перестановка ![]() , а полученная
перестановка
, а полученная
перестановка ![]() , где точками
обозначены все остальные совпадающие элементы. Число инверсий, которые образуют
эти элементы между собой и с элементами i и j , в
подстановках
, где точками
обозначены все остальные совпадающие элементы. Число инверсий, которые образуют
эти элементы между собой и с элементами i и j , в
подстановках ![]() и
и ![]() , совпадает, так как положение
этих элементов между собой и относительно элементов i и j в
подстановках
, совпадает, так как положение
этих элементов между собой и относительно элементов i и j в
подстановках ![]() и
и ![]() не
изменилось. Если i>j то в перестановке
не
изменилось. Если i>j то в перестановке ![]() i
и j образуют инверсию, а в перестановке
i
и j образуют инверсию, а в перестановке ![]() не образуют. Если i<j
то в перестановке
не образуют. Если i<j
то в перестановке ![]() i и j не
образуют инверсию, а в перестановке
i и j не
образуют инверсию, а в перестановке ![]() образуют.
Таким образом число инверсий в перестановках
образуют.
Таким образом число инверсий в перестановках ![]() и
и
![]() отличается на единицу, и
перестановки имеют противоположную четность.
отличается на единицу, и
перестановки имеют противоположную четность.
2. Производится
транспозиция элементов i и j , которые разделены m
элементами перестановки. Пусть ![]() исходная,
исходная, ![]() полученная перестановки:
полученная перестановки:
![]() ,
, ![]() , где точками обозначены все
остальные совпадающие элементы подстановок. Перейдем от перестановки
, где точками обозначены все
остальные совпадающие элементы подстановок. Перейдем от перестановки ![]() к перестановке
к перестановке ![]() при помощи транспозиций
соседних элементов. Сначала переставим элементы i и
при помощи транспозиций
соседних элементов. Сначала переставим элементы i и ![]() местами, затем поменяем
местами элементы i и
местами, затем поменяем
местами элементы i и ![]() , и т.д.
сделав m транспозиций соседних элементов, перейдем к перестановке:
, и т.д.
сделав m транспозиций соседних элементов, перейдем к перестановке:
![]()
Затем переставим элементы i
и j, ![]() и j, и т.д. сделав еще
m+1 транспозиций соседних элементов перейдем к перестановке
и j, и т.д. сделав еще
m+1 транспозиций соседних элементов перейдем к перестановке ![]() . Таким образом от
перестановки
. Таким образом от
перестановки ![]() к перестановке
к перестановке ![]() при помощи 2m+1
транспозиций соседних элементов. Так как каждая такая транспозиция меняет
четность перестановки на противоположную, то перестановки
при помощи 2m+1
транспозиций соседних элементов. Так как каждая такая транспозиция меняет
четность перестановки на противоположную, то перестановки ![]() и
и ![]() имеют
противоположную четность. Теорема доказана.
имеют
противоположную четность. Теорема доказана.
Теорема 3. Для любого числа n>1 число всех четных n-перестановок равно числу всех нечетных перестановок.
Доказательство.
Пусть ![]() и
и ![]() соответственно
число всех четных и нечетных перестановок. Пусть
соответственно
число всех четных и нечетных перестановок. Пусть ![]() любая
из
любая
из ![]() четных перестановка. Проводя в
них транспозиции первых двух элементов
четных перестановка. Проводя в
них транспозиции первых двух элементов ![]() ,
получим
,
получим ![]() различных нечетных
перестановок. Так как всего нечетных перестановок
различных нечетных
перестановок. Так как всего нечетных перестановок ![]() ,
то
,
то ![]() . Проводя аналогичное
рассуждение с нечетными перестановками получим
. Проводя аналогичное
рассуждение с нечетными перестановками получим ![]() .
Из этих двух неравенств следует, что
.
Из этих двух неравенств следует, что ![]() =
=![]() . Теорема доказана.
. Теорема доказана.
Следствие. При
n>1 число всех четных перестановок равно ![]() .
.
2.
Подстановки. Определение 5. Подстановкой n-й степени
называется взаимно однозначное отображение ![]() множества
множества
![]() самого на себя. Обычно
подстановку записывают с помощью двух n-перестановок, записанных одна
под другой:
самого на себя. Обычно
подстановку записывают с помощью двух n-перестановок, записанных одна
под другой:
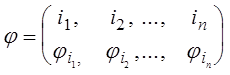 ,
(1) где через
,
(1) где через ![]() обозначается число, в которое
при подстановке
обозначается число, в которое
при подстановке ![]() переходит элемент
i, т.е.
переходит элемент
i, т.е. ![]() ; i=1,2,...,n.
; i=1,2,...,n.
В записи подстановки можно произвольным образом менять столбцы местами. Например, все три указанные ниже подстановки равны.
![]()
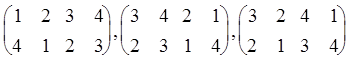 .
(2)
.
(2)
В частности всякая ![]() подстановка n-й степени
может быть записана в виде:
подстановка n-й степени
может быть записана в виде:
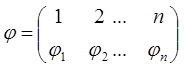 .
.
При такой форме записи различные подстановки различаются только перестановками, стоящими в нижней строке. Тогда в силу теоремы 1 получили следующее утверждение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.