Определители. Перестановки и их четность. Теорема о разложении определителя по элементам ряда, страница 6

= (a₁₁ А₁ + a₁₂(-1)³ А₂  + ...+ a_1n(-1)ⁿ⁺¹ А_n)detB = detA×detB.

Теорема доказана.

6. Вычисление определителей. Определители 2-го и 3-го порядков можно вычислять по правилу Сарюса. Вычисление определителей порядка большего трем сводится к вычислению определителей меньших порядков разложением определителя по строке или по столбцу. Обычно разлагают по тем строкам (столбцам),  в которых имеется много нулей. Для получения нулей используются свойства определителей в частности свойство 8.

Пример 8. Вычислить определитель

.

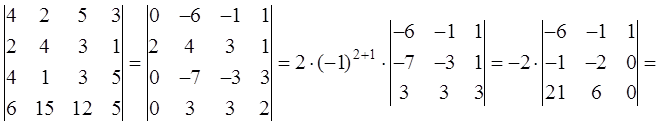
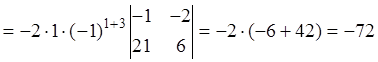При переходе от первого определителя к второму прибавили к 1-й и к 3-й строкам 2-ю, умноженную на -2, к 4-й - 2-ю, умноженную на -3. Затем разложили определитель по первому столбцу. При переходе от третьего определителя к четвертому прибавили к 2-й строке 1-ю, умноженную на -1, к 3-й - 1-ю, умноженную на -3. Затем разложили определитель по третьему  столбцу.

Определители некоторых матриц можно вычислить в общем случае. Например, определители треугольных матриц.

Определение 13. Треугольными матрицами разываются матрицы, у которых все элементы, расположенные по одну сторону от главной диагонали равны нулю, т.о. треугольными матрицами являются следующие матрицы:

.

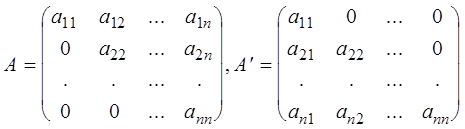Теорема 9. Определитель треугольной матрицы равен произведению элементов главной диагонали, т.е. .

Доказательство. Доказываем методом математической индукции по n. При n=1,2 утверждение теоремы справедливо. Предположим, что теорема справедлива для n-1 и докажем ее для n. Разлагая по первому столбцу, получим:

.

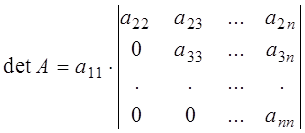Последний определитель по индуктивному предположению равен . Поэтому . Аналогично доказывается и второе равенство. Теорема доказана.

7.Правило Крамера. Рассмотрим систему n линейных уравнений с n неизвестными:

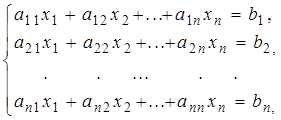                                                      (20) у которой определитель матрицы системы (определитель системы) не равен нулю, т.е.

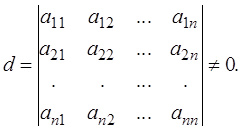
Такую систему называем системой линейных уравнений крамеровсого типа. Далее через  , будем обозначать определитель, полученный из d заменой i-го столбца столбцом свободных членов:

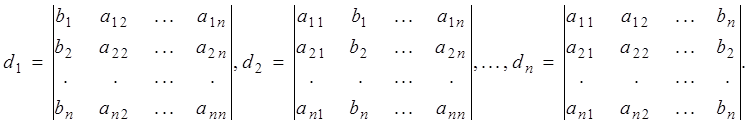
Разлагая определитель ,  по элементам i-го столбца, представим его в виде:

                                     (21)

где , алгебраические дополнения элементов определителя d.

Теорема 10 (теорема Крамера). Система линейных уравнений крамеровского типа  имеет единственное решение, которое находится по формулам:

.                                          (22)

Способ нахождения решений системы n линейных уравнений  с n неизвестными и ненулевым определителем называется правилом Крамера, а формулы  называются формулами Крамера.

Доказательство. Сначала допустим, что   решение системы (20), и покажем, что оно находится по формулам (22). В силу определения системы справедливы верные числовые равенства:      

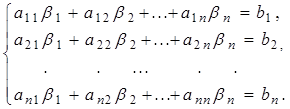
Умножив первое из этих равенств на ,второе на , и т.д. n-е на

и сложив почленно получим равенство:

.

По теореме 6 коэффициент  равен d , по следствию теоремы 6 все коэффициенты у ,..., равны нулю, правая часть равенства по формуле (21) равна  и равенство принимает вид:

.

Аналогично получаем равенства:

Так как , то отсюда находим, что

, т.е. решения находятся по формулам (22).

Покажем, что числа, найденные по формулам (22), удовлетворяют уравнениям системы (20). Имеем

 

.

Эта сумма равна ,  так как по теореме 6 коэффициент у равен d, по следствию теоремы 6 коэффициенты у  ,...,  равны нулю и числа (22) удовлетворяют уравнениям (22). Аналогично устанавливается , что числа (22) удовлетворяют остальным уравнениям системы (20).

Теорема доказана.

Следствие 1. Если система систему n линейных уравнений с n неизвестными не имеет решений или имеет бесконечно много решений, то ее определитель равен нулю.

Действительно, если бы ее определитель был отличен от нуля, то по теореме 9 она бы имела бы единственное решение. Получили противоречие.

Следствие 2. Если система систему n линейных однородных уравнений n неизвестными имеет ненулевое решение, то ее определитель равен нулю.

Действительно, если бы ее определитель был не равен нулю, то по теореме 9 она имела бы единственной нулевое решение. Получили противоречие.

Пример 9. Решить систему

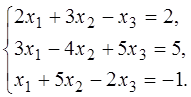
Составим и вычислим определитель системы:

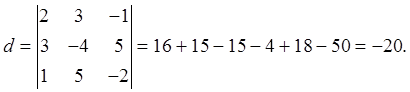
Так как он не равен, то вычислим определители  :

.

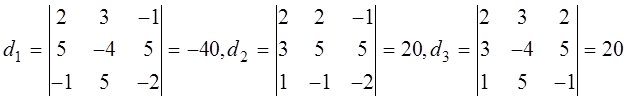Отсюда по формулам Крамера находим:

.

Решение системы (2,-1,-1).