Определители. Перестановки и их четность. Теорема о разложении определителя по элементам ряда, страница 5

для j-го столбца имеем :

.                              (15)

Доказательство. Достаточно в силу замечания 1 доказать теорему для строки. Доказательство состоит из трех частей.

1. Пусть  для всех i=1,2,..,n-1, т.е. определитель имеет вид:

.

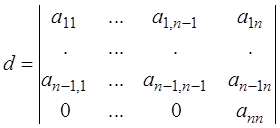По формуле (8) имеем

.

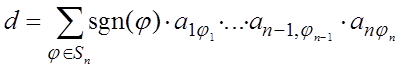Так как =0 для всех , то в сумме выше останутся только такие слагаемые, для которых . Тогда определитель d можно записать в виде:

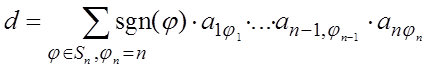.                                 (16)

Тогда 

.                                       

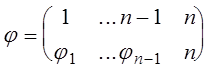Поставим в соответствие подстановке  подстановку

.

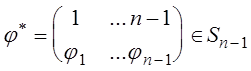Между такими подстановками существует взаимно однозначное соответствие. Далее число инверсий в подстановках  и одинаково. Поэтому  и  сумму (16) можно записать в виде:

.

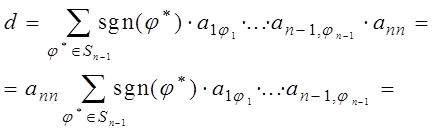
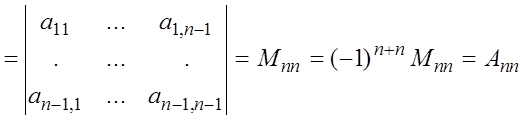2. Все элементы i-й строки равны нулю за исключением элемента ,

.

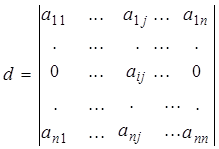Преобразуем этот определитель к предыдущему случаю. Переставим i-ю и  (i+1)-ю строки, затем переставим (i+1)-ю и (i+2)-ю строки и т.д. После n-i перестановок строк определитель по свойству 2 приобретет знак . Затем в полученном определителе переставим j-й и (j+1) столбцы, затем переставим (j+1)-й и (j+2)-й столбцы и т.д. После n-j перестановок столбцов приобретет знак . Тогда после этих преобразований в левом верхнем углу будет стоять минор , а определитель примет вид:

.

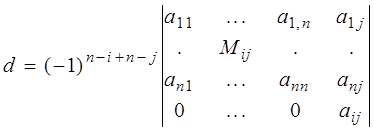Тогда по первому случаю

.

3. Рассматривая общий случай, прибавим к каждому элементу i-й строки  n-1 нулей и разложим полученный определитель на сумму n определителей.

.

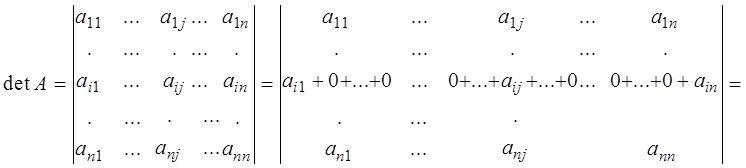
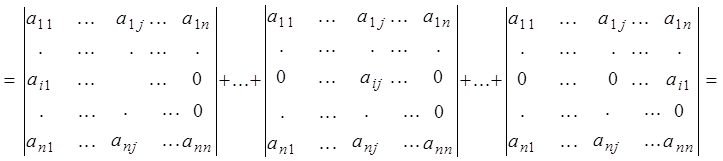
Теорема доказана.

Выделим в определителе i-ю и j-ю строки и разложим определитель по элементам i-й строки:

 ,

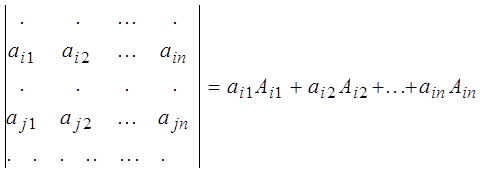где алгебраические дополнения   не зависят от элементов i-й строки. Заменим в обеих частях этого равенства элементы i-й строки на соответствующие элементы j-й строки и получим:

.

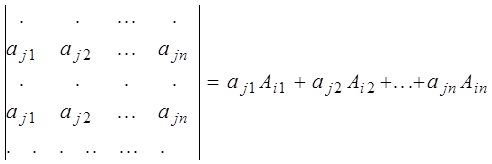Последний определитель имеет две равные строки и поэтому равен нулю. Таким образом получено следствие теоремы 6.

Следствие. Сумма попарных произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения другой строки (столбца) определителя равна нулю, т.е. справедливы формулы:

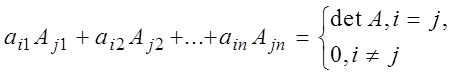
,                           (17)

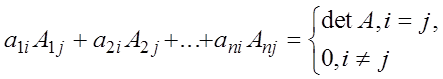
.                             (18)

Замечание 3. Обобщением теоремы 6 является теорема Лапласа, которую мы приведем без доказательства. П.С.Лаплас (1749-1827) - французский математик. Чтобы обобщим понятие минора и алгебраического дополнения.

Определение 12.  Пусть и в матрице A порядка n вычеркнуты k строк с и k столбцов. Минором k -го порядка называется определитель матрицы составленной с сохранением порядка из элементов, стоящих на пересечении вычеркнутых  строк столбцов. Дополнительным минором называется определитель матрицы, составленный с сохранением порядка из невычеркнутых элементов матрицы .

Если вычеркнуты k строк с  номерами   и k столбцов с номерами , то минор и дополнительный минор обозначаем соответственно символами:

.

Алгебраическим дополнением данного минора называется число, которое вычисляется по формуле:

.

Пример 7.

.

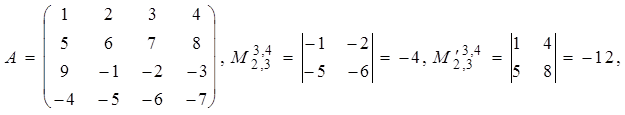
Теорема 7 (теорема Лапласа). Пусть  и в определителе порядка n выбрано k строк. Тогда определитель равен сумме попарных произведений всех миноров порядка k, составленных из этих строк, на их алгебраические дополнения.

Частным случаем теоремы Лапласа является теорема об определителе ступенчатой матрицы. Пусть

,,,

.

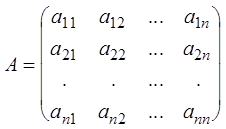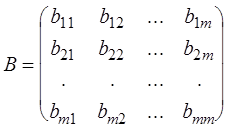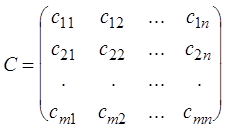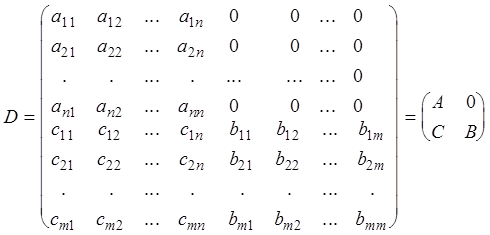Теорема 8 (теорема об определителе матрицы ступенчатого вида). Определитель матрицы D  ступенчатого вида равен произведению определителей матриц А и В, т.е. detD = detA×detB.

Доказательство. Доказываем теорему методом математической индукции по n. При n = 1 утверждение следует из формулы разложения определителя detD по элементам первой строки. Предположим, что утверждение теоремы имеет место для n - 1 и докажем его для матрицы А порядка n. Для этого обозначим через A₁, A₂, ..., A_n и D₁, D₂, ..., D_n -  дополнительные миноры элементов первой строки соответственно матриц А и D. Разложим определитель detD по первой строке:

detD = a₁₁D₁ + a₁₂(-1)³D₂ + ...+ a_1n(-1)ⁿ⁺¹D_n .                         

Каждый из определителей D_i ; i = 1, 2, ..., n, является определителем матрицы ступенчатого вида порядка n + m - 1, в нижнем левом углу которого находится матрица  В , а в левом верхнем углу находится матрица порядка n - 1, определитель которой равен A_i . К определителям D_i применимо индуктивное предположение, т.е. D_i = А_i detB. Поэтому

detD = a₁₁ А₁×detB + a₁₂(-1)³ А₂×detB + ...+ a_1n(-1)ⁿ⁺¹ А_n×detB =