Определители. Перестановки и их четность. Теорема о разложении определителя по элементам ряда, страница 2

Теорема 4. Число различных подстановок n-й степени равно n.

Определение 6. Числом инверсий в подстановке называется сумма числа инверсий в первой и второй строках подстановки.

Обозначаем число инверсий в подстановке  символом  . Подстановка  называется четной, если число   четное, и называется нечетной если число   нечетное. Знаком подстановки   называется число:

.

Таким образом знак подстановки  равен 1 или -1 в зависимости от того четная подстановка   или нечетная.

В силу теоремы 2 при перестановке столбцов в подстановке одновременно четности перестановок, стоящих в нижней и верхней строках подстановки, меняются на противоположные. Следовательно, четность перестановки сохраняется. Отсюда и из теоремы 3 получаем, следующие свойства подстановок.

1. Четность и знак подстановки не зависят от формы записи подстановки .

2. При n>1 число  четных подстановок n-й степени равно числу нечетных подстановок и равно .

Пример 4. Подстановка (2) нечетная и имеет знак -1, хотя при различных формах записи имеет 3, 7, 5 инверсий.

Покажем, что множество всех подстановок n-й степени образует группу относительно операции умножения подстановок, определенной ниже. Эта группа имеет большое значение в алгебре, называется симметрической группой и обозначается символом .

Определение 7.  Произведением подстановок  и   n-й степени называется композиция этих постановок  как отображений, т.е. для любого  имеем . Обозначаем 

Так как композиция двух биективных отображений биективное отображение, то произведение двух подстановок n-й степени есть подставок n-й степени. При практическом умножении подстановок сначала выполняется правая подстановка, а затем левая. Например,

,  .

Теорема 5. Множество  всех подстановок n-й степени образует группу относительно операции умножения подстановок.

Доказательство. В силу сказанного выше операция умножения подстановок бинарная алгебраическая операция. Проверим аксиомы группы.

Умножение подстановок ассоциативно. Действительно, пусть  . Тогда для любого  

 

и по определению равенства отображений .

Единичным элементом является тождественная подстановка

.

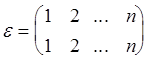Обратной подстановкой для подстановки является подстановка

.

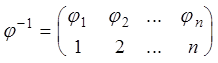Действительно,

.

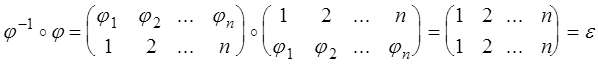Аналогично показывается, что .

Следовательно, по определению множество  группа. Теорема доказана.

Пример выше показывает, что группа  некоммутативная, т.е. неабелева.

3. Определение определителя.  Понятие определителя возникло в связи с задачей решения систем линейных уравнений. Рассмотрим систему двух линейных уравнений с двумя неизвестными:

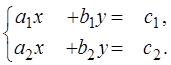                                                                 (3) 

Решим эту систему методом исключения неизвестных. Для этого умножим первое уравнение на  , а второе на ,сложим уравнения и  получим:

 .                                                   (4)

Аналогично, исключая x , получим

.                                                (5)

Выражение  называется определителем квадратной матрицы второго порядка и обозначается специальным символом       

.

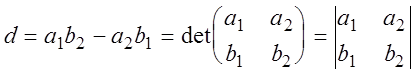Тогда, если через  и  обозначим определители:

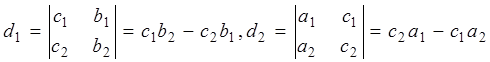, то равенства (4) и (5) перепишутся в виде:

.

Если   , то из них находим

.                                                                   (6)

Нетрудно проверить, что x и y , найденные по формулам (6) , являются решением уравнения (3). Аналогичные формулы имеют место и для систем n линейных уравнений с n неизвестными. Способ нахождения решений уравнения (3) по формулам (6) называется правилом Крамера. Г.Крамер (1704-1752) швейцарский математик, заложил основы теории определителей.

Пусть дана квадратная матрица A порядка n:

.

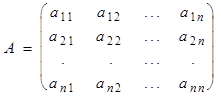Определение 8. Определителем n-го порядка или определителем квадратной матрицы порядка n называется алгебраическая сумма всевозможных произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы со знаком равным знаку подстановки, первая строка которой составлена из номеров строк, а вторая строка составлена из номеров столбцов, из которых взяты элементы, входящие в произведение. 

Обозначается определитель n-го порядка одним из следующих способов:

.

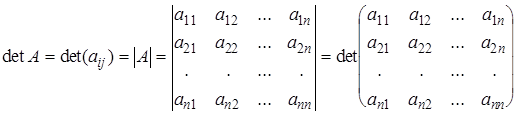По определению  алгебраическая сумма произведений вида:

,                                                              (7)