Определители. Перестановки и их четность. Теорема о разложении определителя по элементам ряда, страница 4

(учитываем, что элемент лежит в определителе  в j-й строке в-м столбце, элемент  -  в i-й строке и в -м столбце). У подстановок  и совпадают вторые строки, а первая строка подстановки  получена из первой строки подстановки  транспозицией элементов i и j . Поэтому в силу теоремы 2 подстановки  и имеют противоположную четность и знак. Отсюда образом  произведение (13) входит в определители d  и  с противоположным знаком. Таким образом определители d  и   суммы одних и тех же произведений, но с противоположными знаками и d= -.   . Свойство доказано.

Свойство 3. Если в определителе есть две одинаковые строки, то определитель равен нулю.

Доказательство.  Пусть в определителе d i-я строка равна j-й строке. Переставим i-ю и j-ю строки местами и получим определитель   (см.(13)). По свойству 2 d= -. Так как i-я и j-я строки равны, то d= . Из этих равенств находим, что d= 0. Свойство доказано.

Свойство 4. Если в определителе есть нулевая строка, то определитель равен нулю.

Доказательство.  Пусть в определителе i-я строка нулевая. По определению определителя он равен алгебраической сумме произведений вида:

.

В каждое произведение входит нулевой элемент i-й строки и поэтому оно равно нулю. Следовательно, и определитель равен нулю. Свойство доказано.

Свойство 5. Если все элементы какой-нибудь строки определителя представлены в виде двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны соответствующим первым слагаемым, во втором - вторым слагаемым.

Пусть все элементы i-й строки представлены в виде ; j=1,2,...,n. Тогда свойство перепишется в виде:

=

=  .

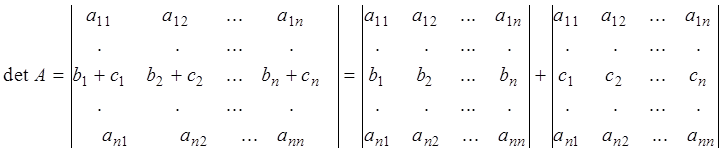Доказательство.  По формуле (8) находим

= .

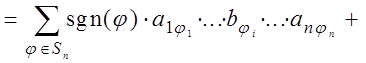
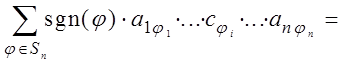
Свойство доказано.

Замечание 2. Индукцией по m легко доказать, что свойство 5 справедливо для случая, когда каждый элемент i-й строки сумма m слагаемых, .

Свойство 6. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя, т.е., если элементы какой-нибудь строки определителя умножить на число k , то и сам определитель умножится на число k.

.

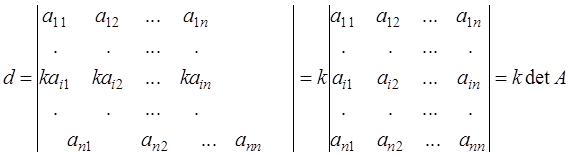Доказательство. По формуле (8) находим 

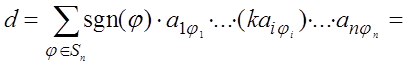
Свойство доказано.

Свойство 7. Если в определителе есть две пропорциональны строки, то он равен нулю.

Доказательство. Пусть i-я и j-я строки определителя пропорциональны, т.е. . Вынося из j-й общий множитель k за знак определителя, получим определитель с двумя равными строками, который равен нулю. Поэтому и исходный определитель равен нулю. Свойство доказано.

Свойство 8. Если к какой-нибудь строке определителя прибавить другую строку, умноженную на число k, то определитель от этого не изменится.

Доказательство. Пусть к i-й строке определителя прибавили ее  j-ю строку, умноженную на число k . Тогда по свойствам 5 и 7 получаем:

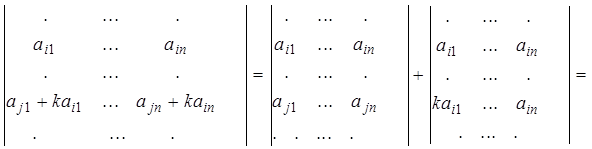
Свойство доказано.

Определение 10. Говорят, что i-я строка матрицы A есть линейная  комбинация остальных строк определителя, если существуют такие числа , что каждый элемент i-й строки есть сумма попарных произведений этих чисел на соответствующие элементы остальных строк матрицы, т.е.

Свойство 9. Если  какая-нибудь строка определителя есть линейная комбинация остальных строк определителя, то определитель равен нулю.

Доказательство. Если  i-я строка определителя есть линейная комбинация остальных строк определителя, то по замечанию 2 определитель равен сумме n-1 определителей с пропорциональными строками, и по свойству 7 все такие определители равны нулю. Тогда и исходный определитель равен нулю. Свойство доказано.

5. Теорема о разложении определителя по элементам ряда. Речь в этом пункте пойдет о выражении определителя n-го порядка (n>1) через определители меньших порядков, что имеет большое значение при вычислении определителей.

Определение 11. Минором (n-1)-го порядка называется определитель матрицы, которая получается из данной матрицы n-го порядка (n>1) вычеркиванием i-й строки j-го столбца. Обозначается такой минор символом  . Алгебраическим дополнением элемента  называется число  .

Пример 6. Для данного определителя найдем , и :

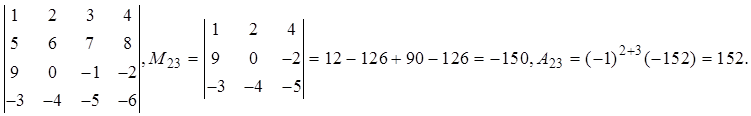
Теорема 6 ( о разложении определителя по элементам ряда). Определитель порядка n>1 равен сумме попарных произведений элементов какой-либо строки определителя на соответствующие им алгебраические дополнения , т.о. для i-й строки имеет место разложение:

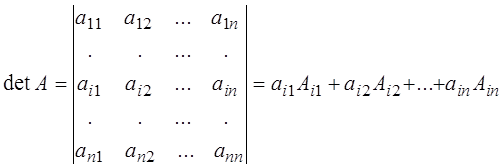,            (14)