где индексы ![]() образуют некоторую
перестановку из чисел 1,2,...,n. Так как по теореме 1 имеется n!
перестановок из n элементов, то определитель алгебраическая сумма n!
произведений вида (7). Для вычисления знака произведения составим подстановку
образуют некоторую
перестановку из чисел 1,2,...,n. Так как по теореме 1 имеется n!
перестановок из n элементов, то определитель алгебраическая сумма n!
произведений вида (7). Для вычисления знака произведения составим подстановку
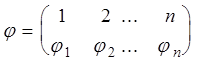
и знак произведения (7) будет
равен знаку подстановки ![]() . Поэтому в
символьном виде определитель можно записать так:
. Поэтому в
символьном виде определитель можно записать так:
![]() ,
(8)
,
(8)
где суммирование ведется по всем n! подстановкам n-й степени.
Покажем, что определитель 2-го порядка вычисляется по формуле:
![]() .
(9)
.
(9)
Действительно, по определению он
равен алгебраической сумме 2!, т.е. 2-х произведений ![]() . Знаки этих произведений равны
соответственно знакам подстановок:
. Знаки этих произведений равны
соответственно знакам подстановок:
![]() , т.е. 1 и -1, что совпадает с их знаками в формуле (9).
, т.е. 1 и -1, что совпадает с их знаками в формуле (9).
Покажем, что определитель 3-го порядка вычисляется по формуле:
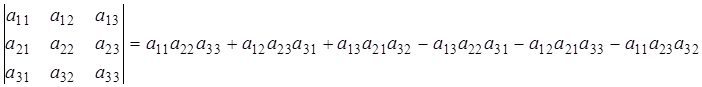 . (10)
. (10)
Действительно, по определению он равен алгебраической сумме 3!, т.е. 6-ти произведений
![]() .
.
Знаки этих произведений равны соответственно знакам подстановок:
![]() .
.
Эти подстановки имеют соответственно 0, 2, 2, 3, 1, 1 инверсий и знаки их соответственно равны 1, 1, 1, -1, -1, -1, что совпадает с их знаками в формуле (10).
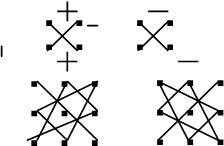 Знаки в формулах (9) и (10)
снабжаются по правилам, которые описываются следующими схемами.
Знаки в формулах (9) и (10)
снабжаются по правилам, которые описываются следующими схемами.
![]()
![]()
![]()
![]() При
n=2
При
n=2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При n=3
На этих рисунках соединены линиями элементы матрицы, составляющие произведения определителя, входящие в него со знаком + и -.
Пример 5.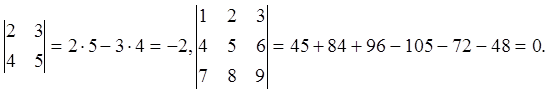
4. Свойства определителей.
Определение 9. Транспонированием A матрицы называется такое ее преобразование, при котором строки матрицы становятся ее столбцами с теми же самыми номерами.
Матрица
транспонированная матрице A обозначается символом ![]() :
:
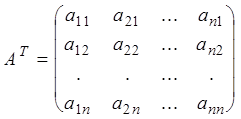 .
.
Свойство 1.
Определитель транспонированной матрицы равен определителю исходной
матрицы, т.е. ![]() .
.
Доказательство. Определителя матрицы А есть алгебраическая сумма n! произведений вида
![]() (11)
(11)
где в каждое произведение входит по одному элементу из каждой строки и каждого столбца матрицы A, со знаком равным знаку подстановки
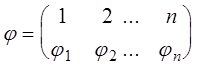 .
.
Так как сомножители
произведения (11) также находятся по одному в каждом столбце и каждой строке
матрицы ![]() , то каждое произведение
определителя матрицы A входит в определитель матрицы
, то каждое произведение
определителя матрицы A входит в определитель матрицы ![]() . Отсюда. так как количество
слагаемых в
. Отсюда. так как количество
слагаемых в ![]() и в
и в ![]() одинаково, следует, что
одинаково, следует, что ![]() и в
и в ![]() состоят из одних и тех же
слагаемых. Для того, чтобы показать, что знаки произведений равны, составим
подстановку для произведения (11) в
состоят из одних и тех же
слагаемых. Для того, чтобы показать, что знаки произведений равны, составим
подстановку для произведения (11) в ![]() (учитываем,
что строки матрицы А стали столбцами матрицы
(учитываем,
что строки матрицы А стали столбцами матрицы ![]() с
теми же номерами). Она равна подтановке:
с
теми же номерами). Она равна подтановке:
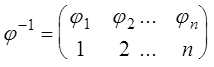 .
.
Подстановки ![]() и
и![]()
![]() имеют одинаковое число
инверсий, четность и знак.
имеют одинаковое число
инверсий, четность и знак.
Таким образом ![]() и
и ![]() суммы
одних и тех же произведений и поэтому
суммы
одних и тех же произведений и поэтому ![]() .
Свойство доказано.
.
Свойство доказано.
Замечание 1. Из свойства 1 вытекает, что строки и столбцы матрицы равноправны, т.е., если какое-нибудь свойство доказано для строк, то оно будет справедливо и для столбцов и обратно. Поэтому дальнейшие свойства формулируются и доказываются только для строк. В дальнейшем под строками и столбцами определителя понимаются строки и столбцы соответствующей матрицы.
Свойство 2. Если в матрице поменять местами две строки, то абсолютная величина определителя не меняется, а знак определителя меняется на противоположный.
Доказательство. Пусть даны исходный и преобразованный определитель:
 . (12)
. (12)
Определитель ![]() получается из определителя d
перестановкой i-й и j-й строк (точками обозначены все остальные
строки, которые в d и
получается из определителя d
перестановкой i-й и j-й строк (точками обозначены все остальные
строки, которые в d и ![]() совпадают.
Требуется доказать, что d= -
совпадают.
Требуется доказать, что d= -![]() .
.
Определитель d есть алгебраическая сумма n! произведений вида
![]() ,
(13)
,
(13)
где в каждое произведение входит по одному элементу из каждой строки и каждого столбца определителя d, со знаком равным знаку подстановки
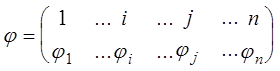 .
.
Так как сомножители
произведения (13) также находятся по одному в каждом столбце и каждой строке
определителя ![]() , то каждое произведение
определителя d входит в определитель
, то каждое произведение
определителя d входит в определитель ![]() .
Отсюда, так как количество слагаемых в d и
.
Отсюда, так как количество слагаемых в d и ![]() одинаково,
следует, что d и
одинаково,
следует, что d и ![]() состоят из
одних и тех же произведений, Для того, чтобы показать, что d= -
состоят из
одних и тех же произведений, Для того, чтобы показать, что d= -![]() , достаточно показать, что
каждое произведение (13) определителях d и
, достаточно показать, что
каждое произведение (13) определителях d и ![]() имеет
противоположные знаки. Знак произведения (13) в определителе
имеет
противоположные знаки. Знак произведения (13) в определителе ![]() равен знаку подстановки:
равен знаку подстановки:
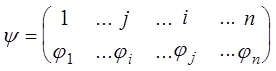
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.