Математика \ Алгебра и геометрия

Векторное пространство. Линейная зависимость. Базис векторного пространства, страница 6

.  .  .  .  .  .  .  .  .  .  .  .  .  .                   

un = t1nv1 + t2nv2 + ... +tnnvn.

Определение 3. Матрицей перехода от базиса v  , к базису u называется такая матрица

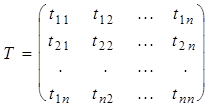, столбцы которой есть соответствующие координатные столбцы векторов второго базиса  u в первом базисе v.

В силу (4) связь между базисами и матрицей перехода можно записать в виде:

 (u1, u2, ..., um) =  (v1, v2, ..., vn) 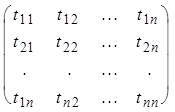, или

u = vT.                                                                             (5)

C другой стороны, если T¢ - матрица перехода от базиса u к базису v , то

v = uT¢.                                                                            (6)

Из (5) и (6) получаем

u = (uT¢)T = u(T¢T)   ,    v = (vT)T¢ = v (TT¢).                                                   (7)

Лемма 1. Пусть А, В матрицы размерности m´n c элементами из поля Р и v = (v1, v2, ..., vn)  - базис n-мерного векторного пространства на Р. Если vA = vB, то A = B. 

Доказательство.  Пусть

, .

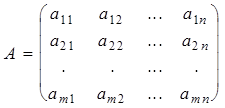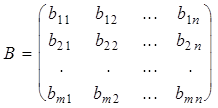Тогда по определениям умножения и равенства матриц равенство vA = vB запишется в виде m векторных равенств:

a1jv1 + a2jv2 + ... + anjvn = b1jv1 + b2jv2 + ... + bnjvn; j = 1, 2, ...,m.

В силу условия равенства векторов, записанных в координатной форме находим aij =  bij; i = 1, 2, ...,n;  j = 1, 2, ...,m. Отсюда A = B. Лемма доказана.

Так как   v = vЕ   и   u = uE , то из равенств (7) по лемме 1 получаем T¢T = TT¢ = Е.  Отсюда detT ¹ 0 , T¢ = T-1 и доказана теорема.

Теорема 3. Матрица перехода от одного базиса к другому является невырожденной матрице. Матрицы перехода от первого базиса ко второму и от второго базиса к первому базису являются взаимно обратными матрицами.

4. Преобразование координат вектора. Найдем связь между координатными столбцами произвольного вектора a в базисах v и u. Пусть (x1 ,x2 ,... ,xn)t и (x1¢ ,x2¢ ,... ,xn¢)t - координатные столбцы вектора a в базисах v и u . Тогда по формуле (3)

a =  v×(x1 ,x2 ,... ,xn)t , a = u×(x1¢ ,x2¢ ,... ,xn¢)t .

Отсюда по формуле (6) находим

a = v×(x1 ,x2 ,... ,xn)t = (uT)×(x1¢ ,x2¢ ,... ,xn¢)t =u(T×(x1¢ ,x2¢ ,... ,xn¢)t)

и по лемме 1

(x1 ,x2 ,... ,xn)t = T×(x1¢ ,x2¢ ,... ,xn¢)t .                                                          (8)

Отсюда по определению равенства матриц получаем систему равенств:

x1  = t11x1¢ + t12x2¢ + ... + t1nxn¢,

x2  = t21x1¢ + t22x2¢ + ... + t2nxn¢,

.  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .                                                                (9)

xn  = tn1x1¢ + tn2x2¢ + ... + tnnxn¢.

Полученные формулы (8) или (9) называются формулами преобразования координат, а матрица T так же называется матрицей преобразования координат.

5. Условие линейной независимости векторов в координатной форме. Рассмотрим систему векторов ai = ai1v1 + ai2v2 + ... +ainvn, i =1, 2, …, k. Составим векторное уравнение

x1a1 +x2a2 + ...+ xkak = 0.                                                               (10)

В силу условия равенства векторов координатной форме уравнение (10) равносильно системе n линейных уравнений с k неизвестными:

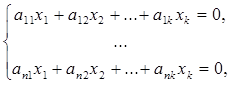                                                       (11)

Система (11) имеет нулевое решение. По теореме Кронекера-Капелли она имеет единственное нулевое решение тогда и только тогда, когда ранг матрицы системы равен k. Отсюда получаем следующую теорему.

Теорема 4. Система k векторов  n-мерного векторного пространства линейно независима тогда и только тогда, когда ранг матрицы, составленной из координат этих векторов в некотором базисе, равен k.

Следствие 1. Упорядоченная система из n векторов  образует базис n-мерного векторного пространства тогда и только тогда, когда ранг матрицы, составленной из координат этих векторов в некотором базисе, равен n.

Ранг квадратной матрицы порядка равен тогда и только тогда, когда определитель матрицы не равен нулю. Таким образом получаем следующее утверждение.

Следствие 2. Упорядоченная система из n векторов  образует базис n-мерного векторного пространства тогда и только тогда, когда равен нулю определитель, составленной из координат этих векторов в некотором базисе.

Скачать файл