Нелинейное программирование. Методы безусловной оптимизации в нелинейном программировании

4.   НЕЛИНЕЙНОЕ  ПРОГРАММИРОВАНИЕ

4.1. Общие вопросы нелинейного программирования

4.1.1. Постановка задачи нелинейного программирования

Задачейнелинейного программирования (НП) называется задача математического программирования, в которой нелинейны или целевая функция или функции, задающие ограничения. (Определение нелинейной функции дано в замечании 1.9) .

Одна из постановок задачи НП имеет следующий вид [23]:

z(X) ® min 

g_j(X) £ 0,      i=1,…, m;                                                           (4.1)

X ³ 0 .                                                   

В этой постановке или z(X), или хотя бы одна  из функций g_i(X) - нелинейные функции n переменных  x₁, … ,x_n.

В постановках задач НП принято указывать требование нахождения минимума ЦФ.  ( В случае необходимости максимизации ЦФ z(X) можно перейти к эквивалентной постановке задачи минимизации функции w(X) = - z(X)).

Необходимо отметить, что различные авторы используют постановки задачи НП, отличные от (4.1) в части ограничений. Так, используются постановки, в которых в состав функциональных ограничений включаются не только неравенства (вида £ или  ³ ), но и равенства  [6, 26, 36, 43]; постановки, в которых отсутствуют непосредственные ограничения [5, 26, 36, 38]; постановки, в которых указаны непосредственные ограничения, задающие диапазоны  допустимых изменений переменных оптимизации [22].                  

Поэтому, несмотря на то, что функциональные ограничения различных видов формально могут быть сведены к ограничениям, использующимся в (4.1), будем в дальнейшем считать, что постановка задачи НП совпадает с общей постановкой задачи математического программирования  вида (1.3) при  b_i=0.

З а м е ч а н и е 4.1.  В постановках задач НП предполагается, что переменные оптимизации непрерывны. Тем не менее, в принципе возможны как задачи нелинейного непрерывного программирования, так и задачи нелинейного дискретного программирования. Задачи второго вида в силу специфики  методов их решения относят к задачам  дискретного программирования.

4.1.2. Задачи НП в САПР

Задачи оптимального проектирования являются типичными задачами нелинейного программирования [36]. При проектировании новых систем всегда определена экстремальная цель (эффективность, надежность, быстродействие и т.д.). Оптимальное проектирование представляет собой процесс определения параметров конструкции, которые экстремизируют эту цель при соблюдении определенных ограничений. В задачах оптимального проектирования целевая функция и ограничения в большинстве случаев являются нелинейными функциями переменных проектирования. В связи с этим методы НП находят широкое  применение в САПР. Они позволяют решать задачи параметрического синтеза объектов и систем в случае, если переменные проектирования – непрерывные величины [22].

Переменным проектирования в рамках методов оптимизации соответствуют переменные оптимизации. При этом ЦФ описывает качество функционирования проектируемой системы или объекта.

Характерной особенностью задач НП, решаемых в САПР, является наличие в них большого числа различного рода ограничений.

При этом в рамках непосредственных (прямых) ограничений помимо традиционных условий неотрицательности, часто используются ограничения вида  d_j £ x_j £ D_j,  d_j £ x_j  или  x_j £ D_j . Поскольку они накладываются на параметры системы, то их называют параметрическими.

Характерно также наличие функциональных ограничений типа равенств или неравенств, которые в рамках САПР трактуются как условия работоспособности  проектируемого объекта [21].

4.1.3. Геометрическая интерпретация целевой функции и ограничений

При рассмотрении методов решения задач НП бывает полезной геометрическая интерпретация компонентов постановки задачи. 

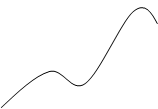
Так, целевая функция, зависящая от одной переменной, может быть представлена на плоскости в виде графика функции z(x) в декартовой системе координат. Непосредственные ограничения вида x ³ a или x £ b представляются в виде полуплоскостей, задаваемых соответствующей граничной прямой. Примеры  такого представления приведены на рис. 4.1.

      а                                             б                                                        в

   z(x)                                             z(x)                                                z(x)    

0    a                        b    x        0    a       x₁              b      x             0     a               x₁          b    x

Рис. 4.1.