Нелинейное программирование. Методы безусловной оптимизации в нелинейном программировании, страница 8

Шаговые методы строятся таким образом, чтобы пределом числовой последовательности {z ^k} было  искомое значение экстремума или оптимума z_опт .

Рассмотрим последовательность точек {Х^k }. Будем трактовать построение такой последовательности точек  как  “движение” точки или как “пошаговое движение” точки в n-мерном пространстве.

           Известно, что точку n-мерного пространства можно представить соответствующим радиусом-вектором. Тогда точки X⁰,X¹,X², …, X^k  можно трактовать как последовательность  радиус-векторов.

Каждый вектор такой последовательности определяется на основании предыдущего вектора той же последовательности следующим образом

X^k+1 =  X^k  +  D(X^k)   ,      k = 0,1,2, …                               (4.11)

где D(X^k) – n-мерный вектор, называемый шагом.

Таким образом, каждый текущий вектор X^k+1 последовательности представляет собой сумму предшествующего вектора  последовательности  X^k и вектора - шага D(X^k).

Для случая трехмерного пространства часть векторов такой последовательности может иметь вид, представленный на рис. 4. 6

                                              Рис. 4.6

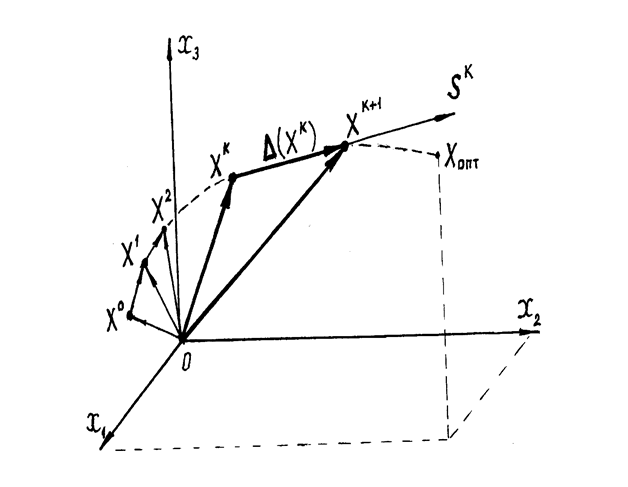
Шаг D(X^k) , будучи вектором, характеризуется величиной и направлением. Поэтому  соотношение (4.8) обычно записывается в более детализированной форме. В ней шаг представляется в виде произведения вектора направления S^k на некоторое число h^k, называемое длиной (величиной) шага:

X^k+1 =  X^k+ h^kS^k   ,     k = 0,1,2, …                                     (4.12 )

Вектор направления изображен на рис. 4.6 (при 0< h^k < 1).

З а м е ч а н и е 4.9. Число h^k часто называют шагом  в направлении S^k или просто шагом. Очевидно, что такая величина является скалярной. Будем все же считать такое сокращение допустимым, но полагать, что термин “шаг” обозначает прежде всего вектор D(X^k).  Будем использовать также понятие “модуль шага”, понимая под этим модуль вектора  D(X^k).

Таким образом, в шаговых методах вычисление очередной точки X^k+1 разбивается на два этапа:

1) выбор направления S_k спуска из точки X^k в сторону уменьшения z(X);

2) определение величины шага спуска h^k.

В соответствии с формулами (4.11) и (4.12) для определения текущей точки  X^k+1  достаточно знание лишь предыдущей точки  X^k . Вместе с тем существует ряд шаговых методов, в которых шаг D(X^k)  рассчитывается учетом нескольких предшествующих точек последовательности. Формально такой шаг представляется в виде D(X^k, X^k-1, …, X^k-r ), где r- число точек, предшествующих последней.

Естественно, что алгоритмы поиска с шагом, вычисляемым таким образом, могут обеспечить более высокую скорость сходимости к экстремуму, поскольку используют дополнительную информацию  об особенностях оптимизируемой функции. 

Следует подчеркнуть, что шаговые методы, реализующие соотношения (4.10), (4.11) и (4.12) обеспечивают нахождение лишь локального  экстремума.

           З а м е ч а н и е 4.10.  Существуют  численные методы оптимизации (так называемые методы сканирования), предусматривающие пошаговое движение в n-мерном пространстве, но не требующие  при таком движении выполнения условия (4.10).

           З а м е ч а н и е  4.11. В значительной части методов помимо шагов, описываемых формулами (4.11) или (4.12), выполняются  шаги, позволяющие оценивать поведение ЦФ в окрестности некоторой точки. Будем называть такие шаги вспомогательными.             

4.2.3.3. Общие проблемы шаговых методов

Как будет показано ниже, шаговые методы отличаются большим разнообразием. При их использовании возникает необходимость в решении одних и тех же вопросов, которые мы будем условно называть проблемами.

1) Проблема начальной точки.

В каждом из рассматриваемых методов итерационный процесс должен начинаться с выбора некоторой точки начального приближения или начальной точки поиска, обычно  обозначаемой символом X⁰.