Целевые функции двух переменных могут быть представлены линиями уровня. Такие линии образуются на основе линий пересечения поверхности, являющейся графиком ЦФ, плоскостями, параллельными плоскости x10x2. Линии пересечения отвечают равным значениям функции z(x1,x2) = c при заданных значениях с.
Линии пересечения проектируются на плоскость x10x2. Их проекции на указанную плоскость и носят название линий уровня. Для описания функции используется некоторая совокупность таких линий, построенная для некоторой последовательности значений с. Если совокупность линий достаточно “частая”, то она наглядно характеризует поведение функции.
Линии уровня представляют собой аналог топографических линий равного уровня на географической карте. В связи с этим топографическая терминология широко используется при описании ЦФ в задачах оптимизации. Так, используются следующие понятия, описывающие “рельеф” целевой функции: “яма”, “котловина”, “впадина” (рис. 4.2,а), “холм” или “вершина” (рис. 4.2.а при c1 > c2 > c3 > … ), “овраг” или “щель” (рис. 4.2, б), “хребет” (рис. 4.2.б при c1 > c2 > c3 > … ), “перевал” или “седло” (рис. 4.2, в), “плоскогорье” и т.д.
Большая часть методов оптимизации НП предусматривает целенаправленное изменение переменных оптимизации в процессе процедуры поиска экстремума. Такие изменения трактуются как движение изображающей точки в пространстве переменных. Если при изменении одного или нескольких значений переменных x1, x2, …, xn наблюдается уменьшение значений ЦФ, то такое движение в пространстве любого числа переменных называется спуском, а в направлении увеличения – подъемом.
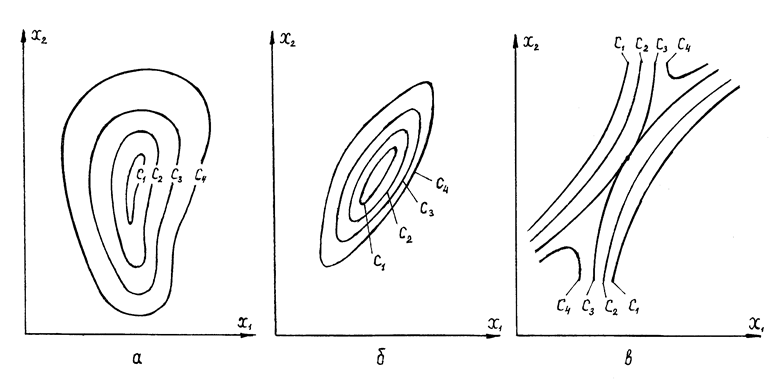
Рис. 4.2 - Примеры рельефов ЦФ (c1 < c2 < c3 < c4 <… )
В плоскости x10x2 можно изобразить также и функциональные ограничения, накладываемые на ЦФ двух переменных.
Пусть, например, ЦФ имеет вид параболоида (точнее, параболоида вращения, смещенного относительно начала координат), пересекаемого плоскостью W, описывающейся уравнением g1(x1,x2)=0. (рис. 4.3.а).
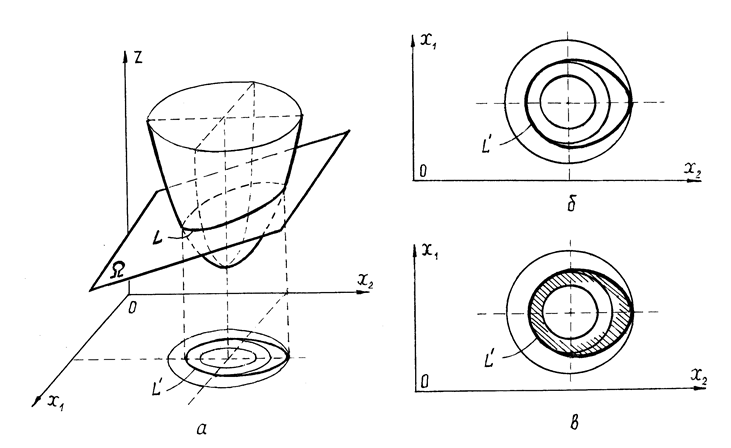
Рис. 4.3
Основой графического представления функциональных ограничений типа равенств является изображение на плоскости x10x2 линии пересечения поверхности, отвечающей ЦФ, и поверхности, задаваемой ограничением-равенством g1(x1,x2)=0. (На рис. 4.3.а такая линия обозначена символом L). Далее такая линия проектируется на плоскость x10x2 путем нанесения на эту плоскость проекций точек, образующихся при пересечении линии пересечения поверхностей с плоскостями, параллельными плоскости x10x2. Таким образом, ограничение типа равенства изображается проекцией линии пересечения. (Такая проекция обозначена рис. 4.3.б как линия L¢).
Ограничения типа неравенств задаются аналогичным образом. При этом для ограничения-неравенства вида g2(x1,x2)£0 рассматривается соответствующее ему уравнение g2(x1,x2)=0 , описывающее “граничную” поверхность. Для такой граничной поверхности, как и в предыдущем случае, формируется линия пересечения и ее проекция (линии L и L¢ на рис. 4.3.в). Для неравенств проекция линии пересечения дополняется штриховкой, указывающей ОДР задачи. (Например, на рис. 4.3.в штриховка на линии L¢ показывает, что неравенству g2(x1,x2)£0 удовлетворяет полупространство, находящееся ниже граничной плоскости g2(x1,x2)=0. Допустимая область задачи тем самым представляет собой нижнюю часть параболоида, отсекаемую плоскостью).
Полезно привести образное представление задачи НП, обобщающее ее геометрическую интерпретацию для случая двух переменных [7]. “Образно говоря, функция цели представляет собой некоторую местность с оврагами, возвышенностями и т.д., а функциональные и непосредственные ограничения – своеобразные изгороди на этой местности. Задача нелинейного программирования состоит в нахождении самой низкой точки местности на территории, окруженной этими изгородями”.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.