Предварительное зондирование ОДП, выполняемое в процессе реализации метода сканирования (как предварительного этапа оптимизации) даже при относительно большом шаге, позволяет выявить особенности ЦФ и определить область глобального экстремума, а также области “тяготения” различных точек ОДП к точкам локальных экстремумов. Таким образом, метод сканирования позволяет решить проблему выбора глобального оптимума из нескольких локальных, а также проблему выбора начальной точки X0. (В качестве X0 может быть принято приближение к точке оптимума, полученное в результате применения метода сканирования).
Метод покоординатного спуска.
(Этот метод называется также методом Гаусса-Зейделя, методом циклического координатного спуска, методом поочередного изменения переменных).
В методе покоординатного спуска поочередно изменяют все переменные оптимизации так, чтобы по каждой из них достигалось наименьшее (наибольшее) значение. (Очередность выбора переменных при этом устанавливается произвольно и обычно не меняется в процессе поиска).
Рассмотрим графическое представление процесса поиска на примере некоторой функции двух переменных, приводимой на рис. 4.8. (На рисунке изображены линии равного уровня некоторой ЦФ (причем a1< a2< a3< a4) а также точка ее минимума Xmin ).
Пусть X0 = (x10, x20) - начальная точка поиска. Выбираем первое направление шагового движения, например, вдоль координатной оси x1. Осуществляем движение изображающей т очки в направлении этой оси до тех пор, пока значение ЦФ уменьшается. Найденная в ходе такого движения точка X1 = (x11, x20) будет отвечать минимуму ЦФ в направлении, задаваемом осью x1. Таким образом, в результате рассмотренного движения в направлении оси x1 будет выполнен шаг D(X0) имеющий длину h1 = | x11 – x 10| .
Далее из точки X1 продолжаем движение к оптимуму в направлении координатной оси x2 . Оно также осуществляется в сторону уменьшения ЦФ и продолжается до тех пор, пока ЦФ уменьшается. Минимум ЦФ в этом направлении достигается в точке X2 = (x11, x22). В результате такого движения выполняется второй шаг D(X1), имеющий длину h2 = | x22 – x20|.
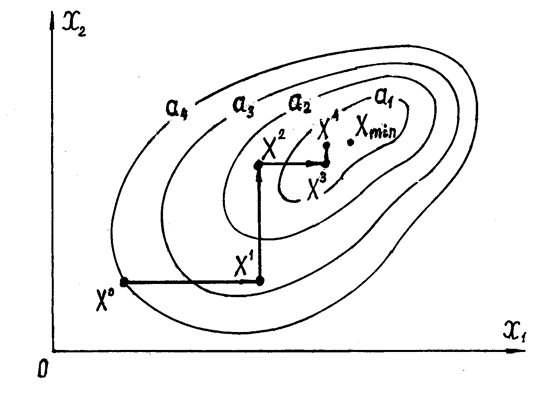 |
После получения точки X2 цикл движений вдоль осей повторяется в той же последовательности. (В случае функции n переменных новый цикл начинается после окончания движений по всем переменным). Построение циклов движений по координатным осям осуществляется до момента выполнения критерия окончания итераций.
Образно стратегию такого поиска (для функции двух переменных) можно определить как действия человека, который, оказавшись на склоне котловины, заросшей густым лесом (не позволяющим ему видеть всю котловину), должен спуститься в ее самую нижнюю точку. Стратегия движения состоит в последовательном спуске к дну котловины в направлениях, определяемых человеком по компасу, попеременно в направлениях Север- Юг и Запад-Восток.
Очевидно, что в рассматриваемом методе векторами направлений Sk являются единичные n-мерные векторы E1, E2 ,…, En.
Рассмотрим более подробно способы организации движения вдоль координатных осей. Определение точки конца шага производится в результате решения вспомогательной одномерной задачи минимизации ЦФ по определенной переменной (при фиксированных значениях других переменных). Такая задача для переменной оптимизации xj на k-ой итерации может быть записана в виде:
z(X(h))j = min (Xk ± h×E j)) (4.16)
h ³ 0
где Ej – единичный вектор направления, соответствующий j-й переменной; h – варьируемая длина шага в направлении j-ой переменной (h > 0). Знак выбирается в соответствии с направлением убывания ЦФ.
Выполненный таким образом шаг часто называют оптимальным. Будем обозначать его символом hопт.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.