Нелинейное программирование. Методы безусловной оптимизации в нелинейном программировании, страница 14

Рассмотрим наглядную иллюстрацию алгоритма симплексного метода на примере отыскания наименьшего значения ЦФ двух независимых переменных с линиями постоянного уровня, изображенными на рис. 4.10

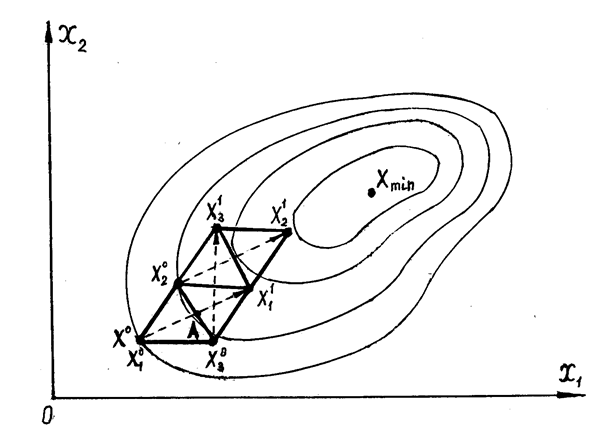
Рис. 4.10

В окрестности начальной точки X⁰ строится начальный симплекс, содержащий точки X₁⁰, X₂⁰,  и X₃⁰ (совпадение начальной точки с одной из точек начального симплекса необязательно). Из найденных трех значений ЦФ выбирается наибольшее. На рис. 4.10. наибольшее  значение ЦФ достигается в вершине X₁⁰. Далее строится новый симплекс, для чего вершина X₁⁰ исходного симплекса заменяется вершиной X₁¹, расположенной симметрично против вершины  X₁⁰. Для варианта, изображенного на рис. 4.10 построение нового симплекса осуществляется определением центра А стороны треугольника X₂⁰X₃⁰ , после чего на продолжении прямой, проведенной через вершину X₁⁰ и точку А, откладывается отрезок  АX₁¹=А X₁⁰. (Стрелка, соединяющая прежнюю вершину с новой, показывает путь преобразования комплекса). В новой вершине X₁¹ вычисляется значение ЦФ, которое сравнивается с известными значениями для других вершин нового симплекса (X₂⁰ и X₃⁰), и снова находится вершина X₃⁰ с наибольшим значением ЦФ, подлежащая исключению при построении следующего симплекса X₁¹X₂⁰X₃¹. Далее строится третий четвертый симплекс X₁¹X₃¹X₂¹ (при условии, что значение ЦФ в вершине X₂⁰, больше, чем в вершинах X₁¹ и X₃¹) и т.д. В результате применения рассмотренной процедуры исключения вершин симплексов с наибольшими значениями ЦФ процесс сходится к ее минимальному значению.

Координаты новой вершины нового симплекса (в векторной форме) определяются по следующей формуле [20,26,44]:    

.                                    (4.17)

               В этой формуле – новая вершина симплекса, n – размерность пространства (число вершин симплекса – n+1),   – вектора вершин симплекса;  – предыдущая вершина,  в которой ЦФ имеет наибольшее значение.

З а м е ч а н и е  4.18. При выполнении вычислений по формуле (4.17) используются  n ее скалярных представлений по каждой переменной оптимизации.

При выходе в район экстремума может возникнуть зацикливание (заключающееся в возврате к предыдущим симплексам). В этом случае необходимо произвести “сжатие” симплекса.  Наиболее просто такое сжатие осуществляется путем откладывания новой вершины относительно центра стороны треугольника на половинную  длину

В этом случае используется следующая формула для вычисления новой точки

 .                                         (4.18)

Процесс сжатия может производиться  многократно. В качестве начального симплекса рекомендуется использование правильного симплекса [26].

З а м е ч а н и е  4.19.  Очевидно, что в рассматриваемом методе при переходе в следующую точку используется информация о поведении ЦФ в трех предыдущих точках (количество дополнительных предшествующих состояний r=3).

На основе базового алгоритмом симплексного метода разработаны несколько модификаций, повышающих его эффективность [54]. Наиболее известной модификацией является метод Нелдера-Мида [35,20]. В этом методе симплекс перемещается с помощью трех основных операций: отражения, растяжения и сжатия (такие операции выполняются с помощью  соответствующих коэффициентов - a, b и g).

При использовании рассмотренных методов используется специальный критерий окончания итераций, учитывающий размеры симплекса (в частности, длину стороны, периметр, расстояние вершин от центра).

Метод Хука-Дживса

(Другое название – метод конфигураций).

Идея метода состоит в том, что для определения направления пошагового движения последовательно выполняются два этапа [20,34]:

1) предварительный (исследующий, вспомогательный) поиск в окрестности начальной базовой точки, позволяющий определить направление дальнейшего поиска,

2) основной поиск (поиск по образцу, рабочий поиск) в направлении, определенном в результате выполнения первого этапа.