Изложенные приемы изображения функций одной и двух переменных, а также наложенных на них ограничений позволяют не только иллюстрировать различные алгоритмы решения задач нелинейного программирования, но и производить графическое решение задачи НП.
4.1.3. Особенности задач НП
Нелинейность функции z(X) и (или) функций gi(X) вызывает существенные отличия задачи (4.1) от задачи линейного программирования. Так, если в задаче ЛП экстремальная точка является крайней точкой многогранника допустимых решений, то в задаче нелинейного программирования она может находиться как на границе ОДР, так и внутри нее.
Указанные случаи (применительно к ЦФ одной переменной) приведены на рис. 4.1. При этом на рис 4.1.а минимум нелинейной функции достигается на границе ОДР в точке a, а на рисунке 4.2 – во внутренней точке ОДР - в точке x1.
Другой особенностью задач НП, вызываемая нелинейностью функции z(X), является ее возможная многоэкстремальность.
Так, на рис. 4.1.в функция одной переменной имеет три минимума. Один из них находится во внутренней точке x1, два других – на концах отрезка. Глобальный минимум расположен в граничной точке а.
Аналогичная ситуация может быть проиллюстрирована и для функции двух переменных. Так, в [4 ] приведен пример многоэкстремальной функции, геометрическое представление которой характеризуется наличием трех “котловин” различной “глубины”. Очевидно, что глобальный минимум достигается в котловине, имеющей “наибольшую глубину”.
Следует заметить, что многоэкстремальность целевой функции создает значительные вычислительные трудности, так как в практических задачах обычно требуется найти среди всех минимумов точку глобального минимума.
Существенно также, что если на каком-то этапе решения задачи оптимизации НП получен оптимальный план, то установить, является ли он локальным или глобальным, можно только путем вычисления значений целевой функции во всех остальных подозреваемых на экстремум точках и сравнения их между собой.
Подавляющее большинство методов оптимизации позволяет находить только локальные экстремумы. Глобальная оптимизация осуществляется значительно сложнее. Для ее выполнения используются специальные методы оптимизации (в первую очередь метод сканирования). В связи с этим проблема локального и глобального оптимумов (минимумов) является наиболее острой проблемой НП.
Нелинейность ограничений также обусловливает особенности задачи НП.
Если в задачах ЛП оптимальное решение отыскивается на конечном множестве крайних точек выпуклой области, то для задачи нелинейного программирования эти условия в общем случае не сохраняются.
Допустимое множество, высекаемое в n-мерном пространстве нелинейными ограничениями, может быть не только невыпуклым, но и несвязным ([ 7 ])
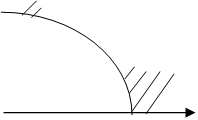
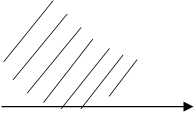
Рассмотрим, например, рис. 4.4. (Напомним, что выпуклой называется область, которая вместе с любыми двумя своими точками содержит и соединяющий их отрезок.)
Рис. 4.4.а иллюстрирует невыпуклую ОДР, а рис 4.4.б - несвязную (состоящую из двух подобластей) Нелинейность ограничений может привести к невыпуклости (рис. 4.4.а) или несвязности (рис. 4.4,б) области допустимых решений,
![]()

![]() а б
а б
![]()

![]()
![]()
 x2
x2
 |
|||
 |
|||
x1 x1
Рис. 4.4.
Эти особенности, отличающие нелинейные задачи от линейных, существенно усложняют их решение и предопределяют ситуацию, состоящую в том, что единого метода решения задач НП нет.
Сложность решения задач НП состоит также и в отсутствии признака, позволяющего судить об оптимальности плана, получаемого в процессе решения задачи. (Напомним, что в ЛП такой признак имеется).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.