Нелинейное программирование. Методы безусловной оптимизации в нелинейном программировании, страница 4

Трудности решения задач нелинейного программирования общего вида заставляют подразделять их на отдельные классы со своими  методами решения. При выделении таких классов важную роль будет играть понятие выпуклости функций.

4.1.4. Выпуклые функции

Функция  f(X), заданная на выпуклом множестве X, называется выпуклой, если для любых двух точек X₁, X₂ Î X и любого l, 0£l£1, справедливо неравенство  

f(X) £ lf(X₁)+(1-l)f(X₂),                                                     (4.2 )

где X= lX₁+(1-l)X₂.

Правая часть неравенства (4.2) представляет собой отрезок прямой, определяемый точками (X₁, f(X₁)) и (X₂, f(X₂)), а левая часть – значение функции в некоторой точке из диапазона возможных значений X Î[X₁; X₂].

Геометрический смысл выпуклости функции поясним применительно к функции одной переменной (т.е. для  X=x), приведенной на рис. 4.5.а. 

Такой рисунок иллюстрирует следующее определение выпуклой функции: функция называется выпуклой, если отрезок,  соединяющий  две  любые  точки  этой  функции,

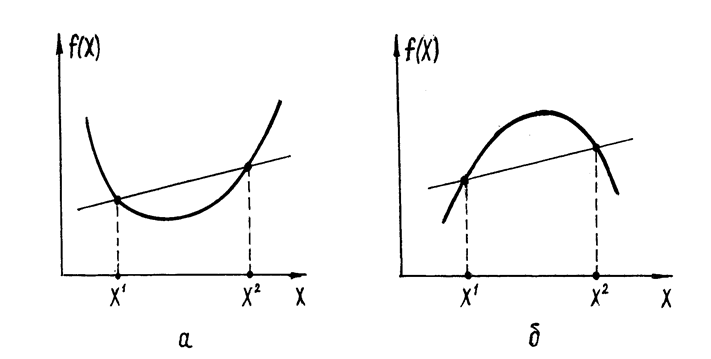
Рис. 4.5

лежит выше  ее значений (такое определение имеет смысл для функций одной и двух переменных).

З а м е ч а н и е  4.2. Поскольку математическое понятие выпуклости плохо согласуется с общеупотребительным понятием выпуклости, то функцию, обладающую свойством, описываемым соотношением (4.2), некоторые авторы называют функцией, выпуклой вниз.

Аналогично определяется понятие вогнутой  функции. Так, функция f(x), заданная на выпуклом множестве X, называется вогнутой, если для любых двух точек X¹, X²ÎX и любого l, 0£l£1, имеет место неравенство

f(X) ³ l×f(X¹) + (1-l)×f(X²),                                                      (4.3)

где X = lX¹ + (1-l)X².

Вид вогнутой  функции  одной переменной приведен на рис 4.5.б. Для нее также может быть дано определение, аналогичное предыдущему, с заменой слова “выше” на  слово “ниже”.

З а м е ч а н и е  4.3. Рис. 4.5 позволяет также проиллюстрировать вид выпуклой и вогнутой функции двух переменных  f(x₁,x₂). При этом плоскость рисунка будет соответствовать плоскости, параллельной оси f(x₁, x₂) и проходящей через отрезок  [X₁ ; X₂].

Очевидно, если f(X) – выпуклая функция, то –f(X) – вогнутая, и наоборот. Линейная функция является одновременно и выпуклой и вогнутой.

Приведенные определения выпуклых и вогнутых функций дают правила для установления их выпуклости. Однако практически использовать эти правила трудно. В ряде частных случаев определение выпуклости или вогнутости функции значительно упрощается.

Так, например, для непрерывных дважды дифференцируемых по всем переменным функций для определения необходимых и достаточных условий их выпуклости используются миноры специально построенной матрицы, называемой матрицей Гессеили гессианом  функции [4].

Такая матрица для функции n переменных z(X) имеет вид

G (X⁰) = 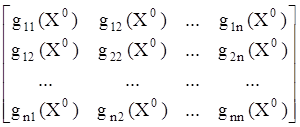                                     (4.4)

 

где                             g_ij (X⁰)=  ,     i=1,…,n ;    j=1,2,…,n.

Таким образом, компоненты матрицы Гессе представляют собой значения вторых частных производных функции z(X), вычисленных в некоторой точке X⁰ .

Необходимым и достаточным условием выпуклости функции z(X) в окрестности точки  X⁰  является неотрицательность всех главных миноров гессиана этой функции, рассчитанных для этой точки [4]. В случае если такие условия справедливы для любой точки  ОДП, считается, что функция выпукла во всей ОДП.

Необходимым и достаточным условием вогнутости функции z(X) является отрицательность нечетных миноров и положительности четных миноров гессиана целевой функции

З а м е ч а н и е  4.4.  Более подробно матрица Гессе будет рассмотрена в приложении  Б.

4.1.5. Типы и виды задач нелинейного программирования.

В нелинейном программировании выделяют два основных типа задач – задачи выпуклого  и задачи невыпуклого программирования.