З а м е ч а н и е 4.14. Рассмотренная классификация по порядку используемой производной не является единственной. Например, методы нулевого порядка называются также прямыми методами или методами прямого поиска.
В связи с введенной классификацией следует заметить, что увеличение порядка метода сопровождается более точным описанием характера поведения ЦФ n переменных в окрестностях точек n-мерного пространства, рассматриваемых в этих методах Наличие большей информации позволяет более эффективно построить процедуру поиска. Таким образом, имеет место следующая тенденция: методы, имеющие больший порядок, имеют большую эффективность.
4.2.3.5. Методы нулевого порядка
Методы нулевого порядка используют в процессе поиска информацию, получаемую при сравнении значений ЦФ, вычисляемых в определенных точках n-мерного пространства. В рамках этих методов выделяются две группы методов: детерминированные (регулярные) и случайные.
Рассмотрим сначала группу детерминированных методов.
Метод сканирования.
Метод сканирования заключается в последовательном просмотре значений ЦФ в ряде точек, принадлежащих ОДП, и нахождении среди этих точек такой, в которой ЦФ имеет минимальное (максимальное) значение.
Основным достоинством метода сканирования является то, что при его использовании с достаточно “густым” расположением точек гарантируется отыскание глобального оптимума. Такое свойство следует из того, что при использовании метода анализируется вся ОДП.
Наиболее простой алгоритм поиска оптимума методом сканирования, называемый поиском на сетке переменных, заключается в том, что по каждой из независимых переменных даются приращения в определенном порядке, обеспечивающем заполнение всей области изменения этих переменных равномерной и достаточно густой сеткой.
В простейшем случае двух переменных сканирование сводится к просмотру значений ЦФ при заданном значении одной переменной (например, x2), для ряда значений другой x1, которые определяются как отстоящие друг от друга на величину шага Dx1 по переменной x1. После того, как весь диапазон изменения переменной x1 при заданном значении x2 исследован и для него найдено минимальное значение ЦФ, изменяется значение переменной x2 также на величину некоторого шага Dx2 по этой переменной и т.д. Графическое представление поиска методом сканирования при двух переменных показано на рис. 4.7.
З а м е ч а н и е 4.15. Хотя в задаче безусловной оптимизации НП отсутствуют ограничения, тем не менее, процедура сканирования всегда осуществляется на некоторой ограниченной области. На рис. 4.7 такая область задается по переменной x1 диапазоном [0; a], по переменной x2 – диапазоном [0 ; b]. В методе сканирования часто производится нормирование переменных, в результате чего они изменяются в едином диапазоне [ 0; 1].
Число вычислений значений ЦФ при определении положения оптимума методом сканирования резко возрастает при увеличении n [26]. Указанная особенность метода является его недостатком. Поэтому эффективное применение данного метода в основном ограничивается задачами невысокой размерности (n = 2…3).
Для сокращения объемов вычислений данным методом разработаны несколько егоj модификаций. Одна из таких модификаций использует алгоритм с переменным шагом сканирования. Вначале величина шага выбирается достаточно большой и выполняется “грубый поиск”, который локализует область нахождения глобального оптимума. После этого производится поиск с меньшим шагом в пределах выделенной области [26].
Метод сканирования в рамках решения задачи оптимизации может использоваться в двух формах: 1) как самостоятельный метод оптимизации, 2) как предварительный этап оптимизации при его совместном использовании с другими методами, реализующими поиск локального экстремума более эффективно, чем метод сканирования.
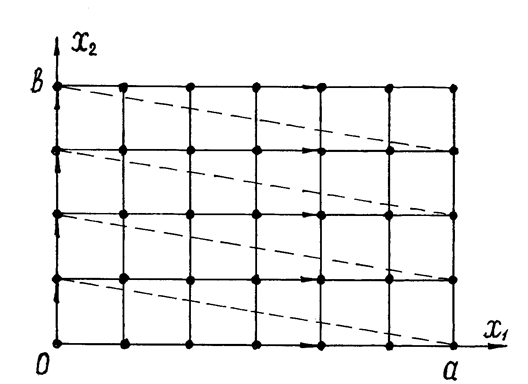 |
Рис. 4.7
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.