В рамках метода покоординатного спуска используются две разновидности решения вспомогательной задачи оптимизации: аналитическим метод решения и численный метод решения. В первом случае используется аналитический метод одномерной оптимизации, рассмотренный в п 4.2.2, во втором - один из численных методов одномерной оптимизации.
Начальным этапом второго метода является пошаговое движение вдоль соответствующей оси в направлении уменьшения ЦФ. Такой шаг h¢ является вспомогательным. Он принимается либо неизменным, либо уменьшающимся от цикла к циклу обхода координатных осей.
В каждой точке получаемой последовательности рассчитываются значения ЦФ и определяется точка, в которой нарушается условие монотонного убывания значений ЦФ. Очевидно, что на интервале между этой точкой и предшествующей ей и находится искомая точка минимума ЦФ в заданном направлении.
Далее, найденная точка может либо рассматриваться как приближенное значение hопт , либо (в соответствии с одним из численных методов одномерной оптимизации) может быть произведено уточнение положения точки, принимаемой за приближение к искомой точке минимума в задаче (4.16).
Графическая иллюстрация решения задачи одномерной оптимизации (4.16) приведена на рис. 4.9. При этом рисунок 4.9.а иллюстрирует аналитический метод решения, а рис. 4.9.б – численный (без уточнения положения точки минимума). (Рисунок изображает вид ЦФ в плоскости, перпендикулярной плоскости x10x2 , параллельной оси Ej и проходящей через точку Xk . Ось координат на рисунке определяется положением точки Xk , а z(X(h=0)) = z(Xk)).
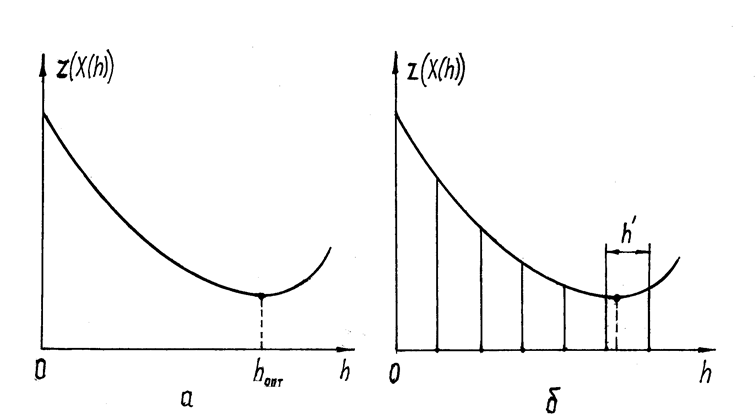 |
Рис. 4.9
Следует отметить, что пониженная точность определения точки hопт численными методами не оказывает существенного влияния на сходимость метода покоординатного спуска.
В связи с этим на практике обычно используются варианты метода, не требующие уточнения положения найденной точки нарушения монотонности. (Более того, в ряде случаев выполняется преднамеренное смещение точки нарушения монотонности в целях повышения эффективности прохождения “оврагов” [54]).
З а м е ч а н и е 4.16. Будем в дальнейшем принимать за точку минимума ЦФ при определении длины оптимального шага средину интервала нарушения монотонности убывания ЦФ.
Эффективность рассматриваемого метода зависит от порядка чередования переменных и от ориентации осей.
Достоинством рассматриваемого метода является простота его реализации, а недостатками - низкая эффективность в “овражных” функциях и существенная зависимость эффективности от выбора системы координат.
Симплексный метод.
(Другие названия метода – метод деформируемого многогранника, метод Спендли, Хекста и Химсворта).
Идея этого метода состоит в том, что по известным значениям ЦФ в вершинах выпуклого многогранника, называемого симплексом, находится направление, в котором требуется сделать следующий шаг, чтобы получить наибольшее уменьшение (при максимизации - увеличение) критерия оптимальности [20,26,54].
З а м е ч а н и е 4.17. Под симплексом в n-мерном пространстве понимается многогранник, имеющий ровно n+1 вершину. Примером симплекса в двухмерном пространстве, т.е. на плоскости, является треугольник, а в трехмерном пространстве – четырехгранная пирамида. Если все вершины симплекса равноудалены друг от друга, то такой симплекс называется регулярным или правильным.
В рамках рассматриваемого метода используется следующее свойство симплекса: против любой из вершин симплекса расположена только одна грань, на которой можно построить новый симплекс, отличающийся от прежнего расположением новой вершины, тогда как остальные вершины обоих симплексов совпадают. При оптимизации интересен случай, когда новая вершина оказывается за гранью или вне симплекса. Это позволяет сделать шаг в n-мерном пространстве.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.