Функциональные последовательности и ряды. Поточечная и равномерная сходимость

14   Функциональные последовательности и ряды

До сих пор мы рассматривали только числовые последовательности и числовые ряды. Теперь будем изучать последовательности, элементы которых – функции, а также ряды, слагаемые которых являются функциями.

14.1   Поточечная и равномерная сходимость

Рассмотрим последовательность функций

f₁(x),    f₂(x),    f₃(x), ..., определённых на множестве   E Í R.  Возьмём какое–либо  aÎE.  Подставляя  a  вместо  х, получим числовую последовательность {f_n(a)}. Она может сходиться, а может и расходиться. Множество чисел  a,  при подстановке которых получается сходящаяся числовая последовательность, называется областью сходимости  последовательности  {f_n(х)}.  Будем обозначать это множество буквой   D:

D = { a  |  {f_n(a)} – сходящаяся последовательность }.

Для каждого aÎD существует конечный предел , который мы обозначим  f(a):

.

Мы употребили функциональную запись f(a) при обозначении числа для того, чтобы подчеркнуть: этот предел зависит от  a,  т.е. это функция от  a. Можно использовать более привычное обозначение переменной:

, не забывая, что  f(х)  определена только на множестве  D. Используется также запись без значка lim: . Такая сходимость последовательности {f_n(х)} к функции f(х) называется  поточечной.  Дадим определение поточечной сходимости на языке  «e–d»:

.

Теперь дадим определение равномерной сходимости, которую будем обозначать так: 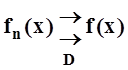  (читается: «последовательность  f_n(х)  сходится равномерно на множестве  D  к функции  f(х)» ).  По определению

.

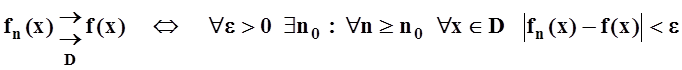На первый взгляд разница в определениях небольшая, однако она существенна. В первом определении требуется, чтобы для каждого хÎD существовал номер n₀ с определённым свойством. Для разных  х  такие номера, возможно, будут разными. Во втором определении – более сильно требование: один и тот же номер  n₀   должен годиться для любого  хÎD.  Таким образом, ясно, что из равномерной сходимости вытекает поточечная:

.

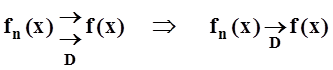Обратное  –  неверно, см. пример 1 ниже.

Дадим геометрическую иллюстрацию к понятию равномерной сходимости. Требование, содержащееся в определении:

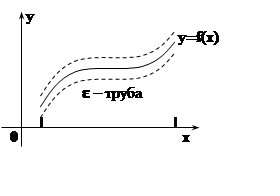
означает, что, начиная с некоторого номера, графики функций f_n(х) мало отличаются от графика  f(х)  на всём множестве D, лежат в  «e–трубе»  графика функции  f(х).  Итак,

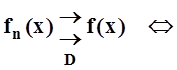
   графики  f_n(х) лежат в  «e–трубе»  графика  f(х).

Пример 1.  Рассмотрим последовательность функций

f₁(x) = x,    f₂(x) = x²,   f₃(x) = x³, ... ,   f_n(x) = xⁿ, ... .

Будем считать xÎD = [0,1]. В каждой точке этого множества последовательность сходится:

Однако эта сходимость не является равномерной. Попробуем понять это, рассматривая графики функций.

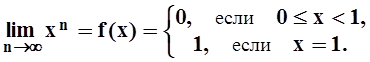
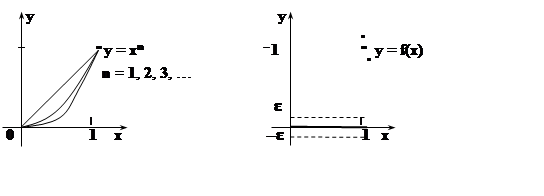Конечно, при любом   xÎ[0, 1]     xⁿ® f(x),   т.е  . "e>0, начиная с некоторого номера n₀,| xⁿ – f(x) | <e. Однако, чем ближе  x  к  1  (но x ¹ 1), тем больший номер  n₀  приходится (для того же e) выбирать. И нельзя взять такое  n₀, которое годится для всех  x. Более того: в этом примере в  «e–трубу»  не попадает ни одна из функций  xⁿ.

Если рассматривать ту же последовательность {xⁿ} на множестве 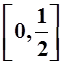, то сходимость будет равномерной. Действительно, в этом случае предельная функция f(x)º0.Так как 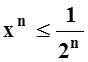    для любого   x  из 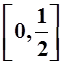 , то достаточно взять  n₀  так, чтобы  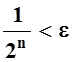 (т.е.   ).  Тогда  "n ³ n₀   неравенство    xⁿ <eбудет выполнено для всех   x из 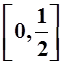  .    Значит,  .

Теперь перейдём от последовательностей функций к рядам. Функциональным рядом называется сумма вида

.

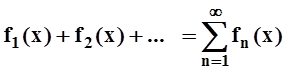Областью сходимости ряда называется множество  D  чисел, при подстановке которых вместо  x  получается сходящийся числовой ряд.

Пример 2.  Найти область сходимости ряда   .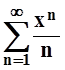

Решение. Зафиксируем  x  и рассмотрим числовой ряд 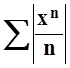 . Вычислим предел:

.

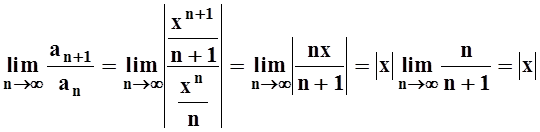По признаку Даламбера, если | x |< 1,  то ряд сходится. Тогда сходится и ряд    (без модулей). Если | x | > 1, то ряд расходится. Причём ряд без модулей    тоже расходится – нарушено  необходимое  условие  сходимости.  Остаётся  проверить две точки:  x = 1,  x = –1.  При   x = 1   получаем    – гармонический ряд,  он расходится.   При  x= –1  получаем    – ряд, сходящийся по теореме Лейбница. Итак, областью сходимости ряда 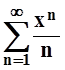   является множество  D = [–1,1).

Обозначим  S_n(x) – частичные суммы ряда  :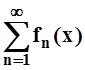

S_n(x) = f₁(x) + f₂(x) + ... + f_n(x).

Если xÎD, то существует . Функция S(x), определённая на области сходимости  D,  называется суммой ряда.  Используется запись :

.

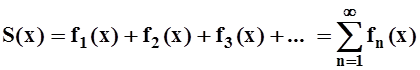Сходимость  ряда к своей сумме может носить разный характер.

Ряд  сходится на D к функции S(x) поточечно, если  S_n(x) ® S(x) поточечно.

Ряд  сходится на D к функции S(x) равномерно , если 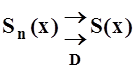. Оказывается, именно равномерно сходящиеся ряды обладают многими хорошими свойствами.

Замечание. Данные определения позволяют свойства рядов выводить из свойств последовательностей. Обратно, для каждой последовательности {g_n(x)} можно рассмотреть ряд

g₁(x) + (g₂(x)–g₁(x)) + (g₃(x)–g₂(x)) + ...  , для которого g_n(x) являются частичными суммами.  Таким образом, многие свойства последовательностей можно сформулировать и на языке рядов, и наоборот. Мы будем пользоваться этим, выбирая наиболее удобный язык.

Теорема 1 (критерий Коши равномерной сходимости).