 Пример
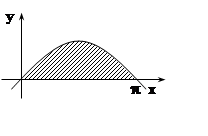
11. Найти статический момент однородной ( r= 1 ) плоской
пластинки, ограниченной линиями y = sinx, y = 0 (0 £ x £ p), относительно оси OY.
Пример
11. Найти статический момент однородной ( r= 1 ) плоской
пластинки, ограниченной линиями y = sinx, y = 0 (0 £ x £ p), относительно оси OY.
Решение.
Элемент пластинки, имеющий координаты (x,
y), имеет площадь dxdy, массу rdxdy,
статический момент относительно OY:
xrdxdy.
Интегрируя, найдём момент всей фигуры: 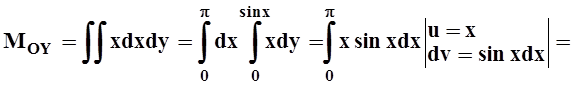
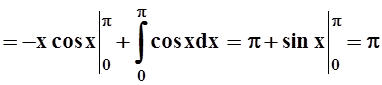 .
.
Центром масс фигуры на плоскости называется такая точка, что если в ней сосредоточить всю массу, то статические моменты этой точки относительно координатных осей будут равны статическим моментам фигуры. Из определения легко следуют формулы для координат центра масс. Например, для плоской фигуры:
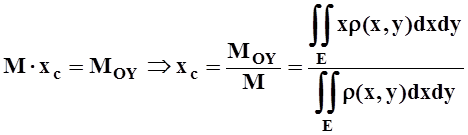 ,
,
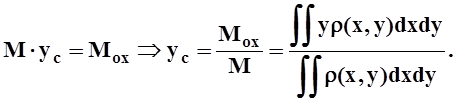
Для фигуры, расположенной в трёхмерном пространстве (тело, поверхность или кривая), статические моменты рассматриваются относительно координатных плоскостей. С их помощью, аналогично плоскому случаю, вводится понятие центра масс. Пусть M, MXOY, MXOZ, MYOZ – масса и статические моменты относительно соответствующих плоскостей. Тогда координаты центра масс, например, материального тела Т вычисляются так:
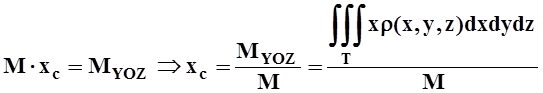 ,
,
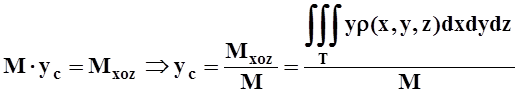 ,
,
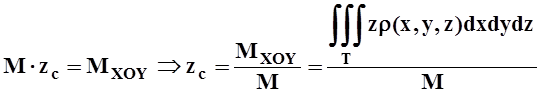 .
.
Для статических моментов и координат центра масс кривой или поверхности формулы те же, меняется лишь тип интеграла.
Пример 12. Найти координаты центра масс тонкого стержня L, расположенного по отрезку прямой x= 2t, y= 3t, z= t, tÎ[0, 1], если плотность r(x,y,z)= x+y+z.
Решение. Так как объект – линия в пространстве, то используется криволинейный интеграл. Найдём массу стержня:
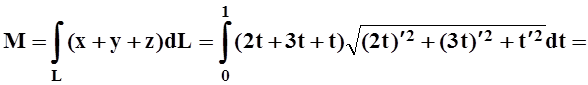
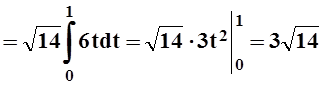 .
.
Найдём статические моменты относительно координатных плоскостей:
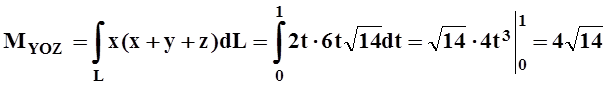 ,
,
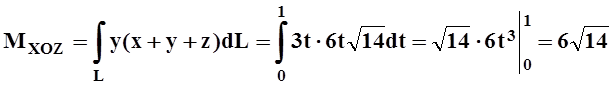 ,
,
![]()
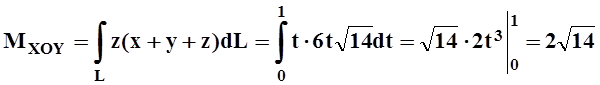 .
.
Теперь находим координаты центра масс:
![]() .
.
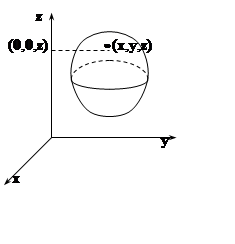 Ещё одно
важное применение интегралов в механике – вычисление моментов инерции. Моментом
инерции материальной точки с массой m
относительно некоторой оси называется величина J = md2, где d–
расстояние до оси. Для системы точек момент инерции определяется как сумма
Ещё одно
важное применение интегралов в механике – вычисление моментов инерции. Моментом
инерции материальной точки с массой m
относительно некоторой оси называется величина J = md2, где d–
расстояние до оси. Для системы точек момент инерции определяется как сумма ![]() . Если же масса не сосредоточена в
отдельных точках, а распределена на некоторой фигуре, то определение даётся с
помощью интеграла (по этой фигуре) от функции rd2
(r–плотность
в текущей точке, d – расстояние от
этой точки до оси). Например, пусть требуется найти момент инерции тела Т относительно оси OZ. Элемент тела с координатами (x,y,z)
имеет массу r(x,y,z)dxdydz. Его расстояние от оси OZ равно
. Если же масса не сосредоточена в
отдельных точках, а распределена на некоторой фигуре, то определение даётся с
помощью интеграла (по этой фигуре) от функции rd2
(r–плотность
в текущей точке, d – расстояние от
этой точки до оси). Например, пусть требуется найти момент инерции тела Т относительно оси OZ. Элемент тела с координатами (x,y,z)
имеет массу r(x,y,z)dxdydz. Его расстояние от оси OZ равно ![]() .
Значит, момент инерции равен
.
Значит, момент инерции равен 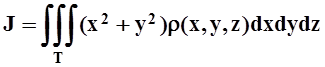 .
.
Можно рассматривать момент инерции относительно точки (полярный момент инерции) или относительно плоскости. В этом случае d– расстояние до соответствующего объекта.
Пример 13. Найти момент инерции однородной (rº1) поверхности параболоида S: 2y= x2+z2, 0£y£2, относительно оси OY.
Решение.
Рассматривается поверхность, поэтому будем применять поверхностный интеграл.
Элемент поверхности с координатами (x,y,z)
имеет массу r(x,y,z)ds= ds, его расстояние до оси
OY равно
![]() . Следовательно,
момент инерции равен:
. Следовательно,
момент инерции равен:

![]() .
.
Будем вычислять поверхностный
интеграл, проецируя поверхность на плоскость XOZ. Проекция есть круг x2+z2£4. Далее, так как ![]() , то
, то ![]() ,
,
![]() , ds=
, ds=![]() dxdz=
dxdz=![]() dxdz. Вычисления удобно
проводить в полярной системе координат:
dxdz. Вычисления удобно
проводить в полярной системе координат:
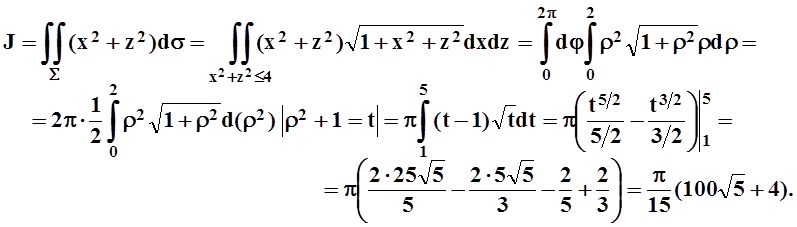
11.6 Задачи с решениями
1. Изменить порядок интегрирования в интеграле
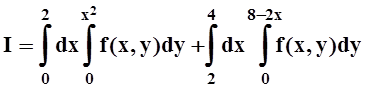 .
.
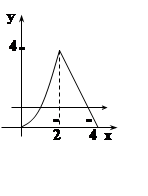 Решение.Изобразим область, по которой проводится интегрирование. В первом
слагаемом 0 £ x £ 2, а y изменяется
от y = 0 (прямая) до
y = x2 (парабола). Во втором слагаемом 2£ x £4,
y изменяется от y = 0 (прямая) до
y = 8– 2x (прямая). Вся
область – объединение этих двух частей. Меняя порядок интегрирования, видим,
что x изменяется от
параболы (на ней
Решение.Изобразим область, по которой проводится интегрирование. В первом
слагаемом 0 £ x £ 2, а y изменяется
от y = 0 (прямая) до
y = x2 (парабола). Во втором слагаемом 2£ x £4,
y изменяется от y = 0 (прямая) до
y = 8– 2x (прямая). Вся
область – объединение этих двух частей. Меняя порядок интегрирования, видим,
что x изменяется от
параболы (на ней ![]() ) до прямой ( на ней
) до прямой ( на ней ![]() ). Пределы внешнего
интегрирования (по y) постоянны: 0£ y £ 4. Итак, изменение порядка интегрирования
позволило заменить сумму одним интегралом:
). Пределы внешнего
интегрирования (по y) постоянны: 0£ y £ 4. Итак, изменение порядка интегрирования
позволило заменить сумму одним интегралом:
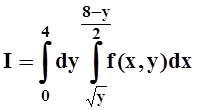 .
.
2.
Вычислить 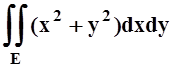 , где область E ограничена одним лепестком лемнискаты
Бернулли (x2+y2)2= 2(x2–y2), соответствующим
x³0.
, где область E ограничена одним лепестком лемнискаты
Бернулли (x2+y2)2= 2(x2–y2), соответствующим
x³0.
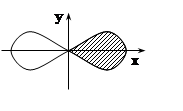 Решение.Запишем уравнение лемнискаты в полярной системе координат (подставляя x= rcosj, y= rsinj ):
Решение.Запишем уравнение лемнискаты в полярной системе координат (подставляя x= rcosj, y= rsinj ):
r4 = 2(r2cos2j–r2sin2j),
r2 = 2cos2j, т.е. ![]() .
.
Теперь легче построить кривую.
Обратим внимание, что в пределах указанного лепестка угол j может принимать значения от ![]() до
до
![]() . Вычисляем интеграл, переходя в
полярную систему координат:
. Вычисляем интеграл, переходя в
полярную систему координат:
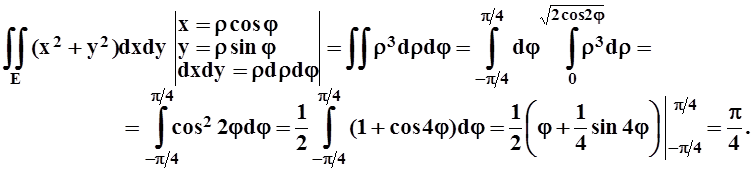
3.
Вычислить 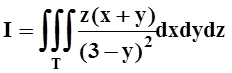 , если тело T ограничено поверхностями z = 0, 3y+z = 9, y = x2–1.
, если тело T ограничено поверхностями z = 0, 3y+z = 9, y = x2–1.
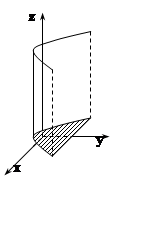 Решение.Сделаем чертёж. Поверхность y = x2–1 – цилиндрическая, направляющей является парабола,
образующие параллельны оси OZ.
Плоскость 3y+z = 9 ограничивает тело сверху, плоскость z = 0 – снизу.
Интегрируя по z, переходим к
двойному интегралу по проекции:
Решение.Сделаем чертёж. Поверхность y = x2–1 – цилиндрическая, направляющей является парабола,
образующие параллельны оси OZ.
Плоскость 3y+z = 9 ограничивает тело сверху, плоскость z = 0 – снизу.
Интегрируя по z, переходим к
двойному интегралу по проекции: 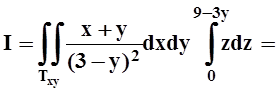
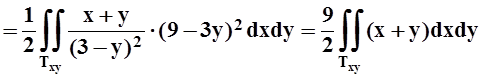 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.