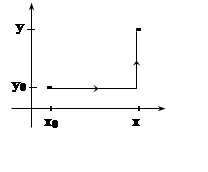
 пути не зависит. Удобно
интегрировать по ломаной, звенья которой параллельны координатным осям:
пути не зависит. Удобно
интегрировать по ломаной, звенья которой параллельны координатным осям:
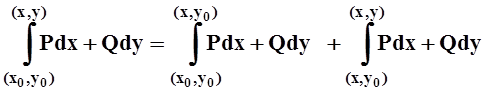 .
.
В первом слагаемом y=y0=const, поэтому dy= 0. Во втором слагаемом x=const, поэтому dx= 0. Значит
U(x,y) =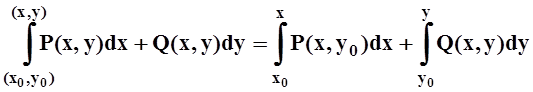 .
.
Выбор начальной точки не играет роли, так как U(x,y) определяется с точностью до произвольного постоянного слагаемого.
Пример 5. Найти потенциал векторного поля
![]() (x,y) = (2x+ 6xy+ 5y3)
(x,y) = (2x+ 6xy+ 5y3) ![]() +(3x2+ 15xy2)
+(3x2+ 15xy2)![]() .
.
Решение. Проверим сначала, что это поле потенциально.
(2x+ 6xy+ 5y3)¢y = 6x+ 15y2; (3x2+ 15xy2)¢x = 6x+ 15y2.
Действительно, по следствию из теоремы 4 поле потенциально. Ищем потенциал по формуле (*). В качестве начальной точки можно взять точку (0, 0). Интегрируя по ломаной, получаем:
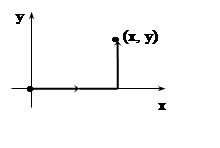 U(x,y) =
U(x,y) =![]() (2x+ 6xy+ 5y3)dx+ (3x2+ 15xy2)dy=
(2x+ 6xy+ 5y3)dx+ (3x2+ 15xy2)dy=
=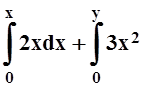 + 15xy2dy=x2+ 3x2y+ 5xy3+C.
+ 15xy2dy=x2+ 3x2y+ 5xy3+C.
Здесь C – произвольная постоянная. При любом другом выборе начальной точки или пути интегрирования получился бы такой же результат.
12.2 Поток векторного поля
12.2.1 Ориентация поверхности. С понятием поверхности мы познакомились ещё при изучении аналитической геометрии. Были рассмотрены алгебраические поверхности 1 порядка (плоскости) и 2 порядка. Далее, при определении площади поверхности, при построении касательной плоскости мы требовали, чтобы поверхность была гладкой. Напомним: если поверхность задана уравнением F(x,y,z) = 0, то гладкость означает, что частные производные F¢x, F¢y, F¢z непрерывны и не обращаются в 0 одновременно. У гладкой поверхности в каждой точке можно построить касательную плоскость и нормаль.
Наиболее просто устроена поверхность S, заданная уравнением вида z=f(x,y). Фактически это график функции 2–х переменных f(x,y), где (x,y) – точка некоторой области E на плоскости XOY. Если G – граница области E, то множество
{ (x,y,z) | z=f(x,y), (x,y) ÎG }
называется краем поверхности S. У такой поверхности, очевидно, имеется 2 стороны: «верхняя» и «нижняя».
Поверхность, заданная уравнением F(x,y,z) = 0, может быть замкнутой – ограничивающей некоторое тело. Такая поверхность тоже имеет 2 стороны: внутреннюю и внешнюю, но не имеет края.
 Постараемся
уточнить понятие «сторона поверхности». Для этого на гладкой поверхности S рассмотрим
замкнутый контур L, проходящий через точку M0ÎS, и не пересекающий
край поверхности. Пусть
Постараемся
уточнить понятие «сторона поверхности». Для этого на гладкой поверхности S рассмотрим
замкнутый контур L, проходящий через точку M0ÎS, и не пересекающий
край поверхности. Пусть ![]() – один из двух
возможных (противоположно направленных) единичных векторов нормали, построенных
в точке M0 к поверхности S. Будем «передвигать»
вектор нормали по L,
меняя точку M на L и строя вектор единичной
нормали так, чтобы он менялся непрерывно. Возвращаясь к точке M0, вектор нормали либо совпадёт с первоначально
выбранным
– один из двух
возможных (противоположно направленных) единичных векторов нормали, построенных
в точке M0 к поверхности S. Будем «передвигать»
вектор нормали по L,
меняя точку M на L и строя вектор единичной
нормали так, чтобы он менялся непрерывно. Возвращаясь к точке M0, вектор нормали либо совпадёт с первоначально
выбранным ![]() , либо будет ему противоположным.
, либо будет ему противоположным.
 Теперь можно
дать определение. Если обход по любому замкнутому контуру (не пресекающему
края) не меняет выбранного направления нормали, то поверхность называется ориентируемой,
или двусторонней. Выбор определённого направления вектора нормали
(в какой–нибудь из точек) равносилен выбору стороны поверхности.
Если же существует контур, обход по которому меняет направление нормали на
противоположное, то поверхность называется неориентируемой, или односторонней.
Примером такой поверхности является лист Мёбиуса, который очень
легко сделать из полоски бумаги, если склеить её концы, предварительно
перекрутив один из них на половину оборота. У листа Мёбиуса всего одна
поверхность, его весь можно покрасить, не отрывая кисточки от бумаги и не
переходя через край. В дальнейшем мы будем рассматривать только двусторонние
поверхности.
Теперь можно
дать определение. Если обход по любому замкнутому контуру (не пресекающему
края) не меняет выбранного направления нормали, то поверхность называется ориентируемой,
или двусторонней. Выбор определённого направления вектора нормали
(в какой–нибудь из точек) равносилен выбору стороны поверхности.
Если же существует контур, обход по которому меняет направление нормали на
противоположное, то поверхность называется неориентируемой, или односторонней.
Примером такой поверхности является лист Мёбиуса, который очень
легко сделать из полоски бумаги, если склеить её концы, предварительно
перекрутив один из них на половину оборота. У листа Мёбиуса всего одна
поверхность, его весь можно покрасить, не отрывая кисточки от бумаги и не
переходя через край. В дальнейшем мы будем рассматривать только двусторонние
поверхности.
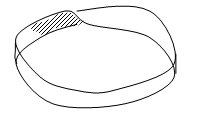
Выберем одну из сторон двусторонней поверхности (или, что, то же самое, определённое направление нормали). Будем говорить, что направление обхода контура, лежащего на поверхности согласовано с выбранной стороной, если из конца вектора нормали обход кажется совершающимся против часовой стрелки.

Здесь
направление обхода и выбор нормали согласованы. Указанный способ согласования
называется правой ориентацией поверхности, он применяется, если в
пространстве выбрана правая системе координат (т.е. орты координатных осей ![]() ,
,![]() ,
,![]() образуют правую тройку).
образуют правую тройку).
Если поверхность замкнутая, то положительным будем считать внешнее направление нормали, не согласовывая его с обходом каких–либо контуров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.